


Next: Document Structure
Up: Mathematics
Previous: Mathematics
In general, quality typeset mathematics looks
quite a bit different than plain typeset text. LATEX will take care
of most of the little details--such as the amount of space to leave around
a plus sign--for you. Since LATEX decides on the proper spacing, it
completely ignores spaces in math mode. (If you are
in math mode and want to include some regular text with regular spacing,
you can use the \text command. The parameter of this command
is typeset as regular text.) You can also use the ``\ '' command
(backslash followed by a space) in math mode for a space that
won't be ignored. And there are a few commands for adding smaller
amounts of space in math mode: \, and \;.
Mathematical operators such as  ,
,  ,
, 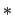 ,
,  ,
, 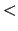 ,
,  , and
, and 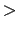 will behave as you expect in math mode. Set braces in math mode,
as in regular text mode, must be types as
will behave as you expect in math mode. Set braces in math mode,
as in regular text mode, must be types as \{ and \}.
The Greek letters are specified by commands that are the same
as the name of the letter: \alpha, \beta, \gamma,
\delta, \epsilon, \theta, and \gamma will
output  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  ,
for example. Capitalized Greek letters use capitalized commands so that
,
for example. Capitalized Greek letters use capitalized commands so that
 and
and  are typed as
are typed as \Sigma and \Phi.
There are many commands that produce special mathematical characters.
A sample is shown in this table:
\le |
 |
\ge |
 |
\ne |
 |
\to |
 |
\cup |
 |
\cap |
 |
\in |
 |
\subset |
 |
\emptyset |
 |
\wedge |
 |
\vee |
 |
\lnot |
 |
\forall |
 |
\exists |
 |
\oplus |
 |
\rightarrow |
 |
\Rightarrow |
 |
\therefore |
 |
\infty |
 |
\partial |
 |
\approx |
 |
Subscripts and superscripts are specified using the special characters
_ and ^. These commands act like commands whose parameters
are put into the subscript and superscript positions. For example,
$a_{i}$ is typeset as  , while
, while $x^{17}$ yields  .
You can combine subscripts and superscripts:
.
You can combine subscripts and superscripts: $x_{i}^{n}$
comes out as  . (Note that you can omit the { and } around
the parameter if the parameter consists of a single character. However,
be aware that if you type
. (Note that you can omit the { and } around
the parameter if the parameter consists of a single character. However,
be aware that if you type $x^17$, you will get  because only
the 1 is in the superscript.) Subscripts and superscripts can be
complicated and can even include other levels of scripting.
So, you can have
because only
the 1 is in the superscript.) Subscripts and superscripts can be
complicated and can even include other levels of scripting.
So, you can have
 , which is typed as
, which is typed as $x_{b^2+a_i^j}$.
To take the square root of something, use \sqrt, which applies the
square root sign to its parameter. For example, type $\sqrt{x^2+1}$
to get
 . The
. The \frac command takes two parameters
and makes them into a fraction in which the first parameter is the numerator
and the second is the denominator. So, $\frac{n+1}{n}$ will
give
 .
. \frac is the first example we've encountered
that looks different in display math mode. Typing $$\frac{n+1}{n}$$
will give the displayed fraction
in which the characters
are much larger. In some cases, you would like to have some in-line
math look like displayed math. You can get this effect by adding
the \displaystyle command. So, you can get
 by typing
by typing $\displaystyle\frac{n+1}{n}$.
Similarly, you can use \textstyle to force display mode math
to be rendered in the style of in-line math.
The summation, product, and integral signs are written as
\sum, \prod, and \int. Subscripts and
superscripts work in a special way with these symbols to add
the usual ``decorations'' at the top and bottom of the symbol.
For example, $$\sum_{n=1}^{\infty}\,\frac{x^n}{n!}=e^{x}$$
is rendered as
Rendered as in-line math, this would be
 . This is one
case where I definitely prefer to use display style.
. This is one
case where I definitely prefer to use display style.
The names of mathematical functions such as sin and ln should
properly not be in italics. LATEX defines commands
for many function names so that they can be typeset properly.
So, for example, you should type \sin(x) to get
 . Certain commands, such as
. Certain commands, such as \lim, use
subscripts in the same way as the \sum command.
For example, $$\lim_{x\to\infty}x^{-x}=0$$ gives
Mathematics makes extensive use of bracketing symbols such as
(, ), [, ], {, }, 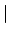 , and
, and 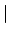 . (The
. (The  ,
,  , and
, and 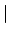 are
typed as
are
typed as \{, \} and \|. You can only
use | and \| in math mode.)
All these symbols should change size according to the size
of the stuff inside the brackets. LATEX uses the
commands \left and \right to make bracketing
symbols that will change size. These commands are used
with bracketing symbols: \left(, \right],
\left\{, \right\|. \left and
\right must always occur as a pair, although the
type of bracketing symbol on the left and right don't
have to match. LATEX will choose the appropriate size
of the brackets.3
There are many other, more sophisticated aspects of
mathematical typing. Some of these are provided by
LATEX environments. I give one example here.
If you want to learn more, you will have to consult
a reference. The array environment can be
used to typeset arrays. An array environment begins
with something like \begin{array}{ccc}. The ``ccc''
says that the array will have three columns and that the
items of the array will be centered in each column. Replace
a c with an l or an r to get left- or right-justified items.
The end of the array is marked with \end{array}.
In the array environment, lines of the array are separated by
\\, and the items on a line are separated by &.
The array is not automatically enclosed in parentheses.
Use \left( and \right) to get that effect.
Here is an array example:
| Input |
Output |
|---|
 |
 |
This array uses \cdots and \vdots
to represent groups of three dots. These commands
are treated just like other array items. The blank
space in the middle of the array is an empty item.
Note that in the source code this blank item
is indicated by two &'s with nothing between
them.



Next: Document Structure
Up: Mathematics
Previous: Mathematics
David Eck
2003-10-21


