CPSC 120, Fall 2002
Second Test, November 20
This is the third test from CPSC 120:
Principles of Computer Science, Fall 2002.
Answers given here for
essay-type questions are sample answers only.
Other answers can also
receive full credit.
Question 1:
Define each of the following terms, as they relate to this course:
a) recursion
b) rendering
c) key frame animation
Answer:
a) Recursion refers to using a subroutine in its own definition. That is, a subroutine is said to be recursive if it calls itself (directly or indirectly).
b) Rendering is the process of creating an image of a scene by deciding how to color each individual pixel.
c) In key frame animation, properties of objects such as position, size, and color are set in a few "key" frames. The computer calculates the properties for other frames by interpolating between the specified key frame values. This makes it much easier to produce animations than it would be if you had to specify every frame individually.
Question 2: Describe the animation that is produced by the following xModels program. Include in your answer a drawing of at least one frame.
animate 30
DEFINE oneThing [
line xtranslate 0.5 scale 3
square rotate 0:360 xtranslate 3
]
DEFINE threeThings [
oneThing
oneThing rotate 120
oneThing rotate -120
]
threeThings rotate 0:120
Answer: The first DEFINE says that oneThing is a line with a square rotating on one end of the line. The center of the square is at one endpoint of the line, and the other end point is at the origin. The second DEFINE says that threeThings consists of three copies of oneThing. Two of the copies are rotated so that all the angles between the lines are equal to 120 degrees. This gives an object consisting of three lines radiating out from the origin, with a rotating square at the end of each line. Finally, the last line displays an object of this type and makes the whole thing rotate about its center. Here is one frame from the animation:
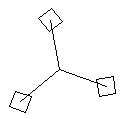
Question 3: (a) Write an xTurtle subroutine named lines with one parameter so that for any positive integer N, the statement lines(N) will draw N parallel lines. Each line should be 5 units long, and the lines should be 1/2 unit apart. For example, lines(6) would draw the picture shown.

(b) Given the subroutine that you wrote for part a, draw the picture that would be produced by the following commands:
lines(4) turn(90)
lines(4) turn(90)
lines(4) turn(90)
lines(4) turn(90)
Answer: (a) There are many variations. In all these variations, a LOOP is used to draw N lines. The main difference from one version to another is where the turtle ends up (although you could get even more variation by using move commands instead of forward and turn). Here are three solutions.
SUB lines(N) SUB lines1(N) SUB lines2(N)
DECLARE ct DECLARE ct DECLARE ct
ct := 0 ct := 0 ct := 0
LOOP LOOP LOOP
forward(5) forward(5) forward(5)
back(5) back(5) ct := ct + 1
ct := ct + 1 PenUp EXIT if ct = n
EXIT IF ct = N turn(-90) back(5)
PenUp forward(0.5) PenUp
turn(90) turn(90) turn(-90)
forward(0.5) PenDown forward(0.5)
turn(-90) ct := ct + 1 turn(90)
PenDown EXIT IF ct = N PenDown
END LOOP END LOOP END LOOP
END SUB END SUB END SUB
lines(4) turn(90) lines1(4) turn(90) lines2(4) turn(90)
lines(4) turn(90) lines1(4) turn(90) lines2(4) turn(90)
lines(4) turn(90) lines1(4) turn(90) lines2(4) turn(90)
lines(4) turn(90) lines1(4) turn(90) lines2(4) turn(90)
(b) The picture for part b depends on the exact answer to part a. here are the pictures produced using the three solutions given above:
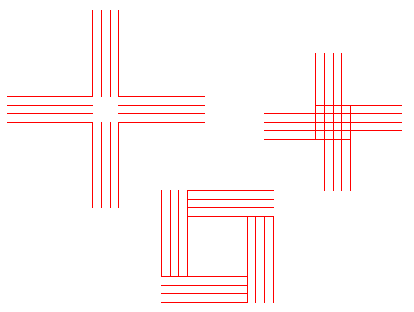
Question 4: Write an xModels program that will draw the following picture:
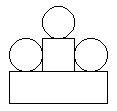
Answer: As usual, there are many variations. Here is one of the simplest, which assumes that the circles and square have their default size of 1. In this solution, the only scaling that is necessary is to change a square into a 3-by-1 rectangle:
square
square scale 3,1 ytranslate 1
circle ytranslate 1
circle xtranslate 1
circle xtranslate -1
Question 5: (a) Parameters are an important aspect of subroutines. What are they, and why are they so important?
(b) There are two types of parameters, actual parameters and dummy parameters. Explain the difference.
Answer: (a) Parameters are used for communication between a subroutine and the rest of the program. A value is provided for a parameter when the subroutine is called. This is important because it allows the subroutine to do different things, depending on the value of the parameter. For example, in forward(N), the distance that the turtle moves depends on the value of N. Without parameters, you would need a different subroutine for every possible distance!
(b) A dummy parameter is used in the definition of the subroutine. For example, in question 3, the N in "SUB lines(N)" is a dummy parameter. A dummy parameter does not have a value and is only a placeholder for the actual parameter. The actual parameter is provided when the subroutine is called. For example, in the subroutine call statements "lines(x)" and "lines(4)", x and 4 are actual parameters.
Question 6: "Write modular programs" is good advice in all parts of the software life cycle. What are modules, and why do they make it easier to develop and maintain programs.
Answer: A module is a component of a system that is relatively independent and that interacts with the rest of the system in straightforward, easy-to-understand ways. Because they are fairly independent, it is possible to develop and test modules separately and then assemble them later into a complete system. For example, this makes it possible for different people to work on different modules. It is also easier to maintain a system if it is made of modules: If one module needs to be replaced because it contains an error or because it is out of date, this can be done without changing all the other components of the system.
Question 7: The xModels program works with simple wireframe models, but one of the goals of 3D graphics is to produce realistic images. Discuss some of the techniques that are used to make realistic images.
Answer: Wireframe models can show the "geometry" of a 3D scene, but they do not look like real objects. For more realistic graphics, you have to draw solid objects that have color, texture, and transparency. You have to include the effects of lighting, such as ambient illumination, shadows and variation in color due to the angles at which light hits the objects. For more realism, you can use more advanced rendering methods such as ray tracing and radiosity.
Question 8: Consider the following recursive xTurtle subroutine:
SUB guess( size, complexity )
forward( size )
IF complexity > 0 THEN
guess( size/3, complexity-1 )
END IF
turn( 120 )
forward( size )
IF complexity > 0 THEN
guess( size/3, complexity-1 )
END IF
turn( 120 )
forward( size )
IF complexity > 0 THEN
guess( size/3, complexity-1 )
END IF
turn( 120 )
END SUB
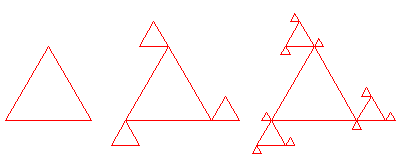
For parts a, b, and c, show the picture that would be produced by the given subroutine call statement.
(a) guess(9,0)
(b) guess(9,1)
(c) guess(9,2)
For extra credit: Find a formula for the number of lines that are drawn during the execution of guess(9,N) for any non-negative integer N. That is, how many times is the forward command executed. Justify your answer.
Answer: For part a, complexity is 0, and the subroutine is equivalent to saying "forward(3) turn(120)" three times. This draws an equilateral triangle. In part b, a smaller triangle is added to each tip of triangle in part a. Part c adds another level of triangles. Here are the pictures for parts a, b, and c:
For the extra credit question, the answer is 3 + 32 + ... + 3N+1. One way to see this is that when the complexity goes up by one, a new set of triangles is added to the picture. The number of new triangles is three times the number of new triangles in the previous picture. So, the number of new triangles for N=2 is 3. The number for N=3 is 32, the number for N=4 is 33, and so on. Since this only counts new triangles, the total number of triangles is the sum 1 + 3 + 32 + ... + 3N. Each triangle contains three lines, so the total number of lines is 3 times this amount.