CPSC 124, Fall 2001
Programming Assignment 2
This is an individual programming assignment. You can get help from me and from the TA on this assignment. Otherwise, you should work on the assignment on your own. You are not permitted to look at other students' programs or to get help on the assignment from them or to help other students.
The assignment is due on Monday, October 29. If you turn it in up to one week after than date, a late penalty of 20% will be deducted from the grade. Assignments will not be accepted after November 5 . If you have done some work but do not have a working program, you should turn in what you have for partial credit.
You should copy your program (both source code and class file) along with all the support files that it needs to run into your cs124_homework directory. I expect to be able to find your program in this directory and run it there. You should also make a printout of your program for me.
For this assignment, your program will be a simulation of something called a drunkard's walk. (Often this is called a "random walk", which is perhaps more politically correct.) In a drunkard's walk, the drunkard starts out at a random point. At each time unit, the drunkard takes one step in a randomly chosen direction. The question is, how far will the drunkard travel after a given number of steps? Of course, the distance traveled will depend on the particular path that the drunkard takes, so we should really ask, what is the average distance traveled by a drunkard after a given number of steps. To investigate this question, you will run a large number of drunkard's walk experiments and compute the average distance traveled. (The drunkard's walk, by the way, is related to more important physical processes such as diffusion and Brownian motion.)
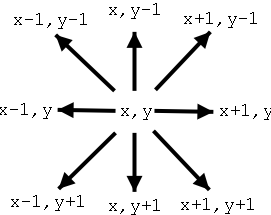To keep things simple, we will assume that the drunkard's position
is given by two int values, x and y. At each
step, the drunkard can move in one of eight directions, chosen
at random. This will change the values of x and y
as shown in the diagram at the right.
To make things more interesting, you will show the user a visual representation of the experiments as they are being run. The visual representation will use the Mosaic class that was used in Lab 6 and in Section 4.6 of the text. Because you want to do a large number of walks, you won't show the drunkard moving. Instead, you want to present a visual representation that will show the user where the drunkard tends to end up at the end of the walk. Start the drunkard at the center of the mosaic. After the drunkard has completed the specified number of steps, make the square where the drunkard ends up a little brighter. After a large number of experiments have been run, the brightest squares are the ones where the drunkard has the highest probability of ending up at the end of his walk.
You can run my program to see how this works. The compiled class file is in the directory /home/cs124/assg2 and is named VisualDrunk.class. You can do cd /home/cs124/assg2 to move into that directory and then do java VisualDrunk to run the program. You will be asked to enter the number of steps that the drunkard should take. Try it with 50 steps. As the experiments are run, you will see red squares appear and brighten. If you let the program run for a while, the squares will brighten further through shades of yellow and then white. After a square becomes pure white, it won't change any further. (Although my program allows you to use a number of steps up to 1000, you will find that with numbers much greater than 100, you'll have to wait a long time before you see the red squares appearing.)
You might want to copy the folder /home/cs124/assg2 into your home directory and work in your copy of that directory, since it already contains all the extra class files that are needed for the program.
Here are some requirements for your program:
- You must define and use a subroutine makeBrighter(row,column) that will increase the brightness of the square in the mosaic at the given row and column. It should implement the following algorithm (or something similar but at least as complicated, if you want to use a different pattern of colors): If the red component of the color of the square is less than 255, it should add 5 to the red component (and leave blue and green unchanged). Otherwise, if the green component is less than 255, it should add 5 to the green component. Otherwise, if the blue component is less than 255, it should add 5 to the blue component. (If all three components are 255, then the color will be left unchanged. Alternatively, in this case, you could try resetting all the colors to 0 so that the square will start again at black.)
- You must have a subroutine doOneWalk(startx,starty,numberOfSteps) which does one drunkard's walk experiment. It should start the drunkard at position (startx,starty). Then it should simulate a random walk for numberOfSteps steps, as described above. At the end of the walk, it should call the makeBrighter() subroutine to increase the brightness of the square where the random walk ends. Furthermore, it should return the distance between the starting point and the ending point of the walk, as a value of type double.
- Your program should ask the user to specify the number of steps for the walk, and you should restrict the number to some reasonable range of values. Open a Mosaic window and call doOneWalk() over and over until the user closes the mosaic window. At that point, you should print out the average distance traveled by the drunkard. You should then give the user the option of repeating the process with a new number of steps.
I encourage you to use other subroutines besides those that are required. Your program should, of course, follow the rules of good programming style, as discussed on the lab worksheets and in class.
This assignment is about subroutines, not objects. There is no need to use any objects in your program. Remember that you are writing a main program, not an applet, so you will run it with the java command, not with appletviewer. Also, all the subroutines that you write must be static. The formula for the distance between two points (x1,y1) and (x2,y2) is Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)).
By the way, at the end of your program, you should call System.exit(0). If you don't do this, you will have to use CONTROL-C to end the program. The reason for this is a little obscure: When you open a window, Java's GUI system starts up, and it doesn't quit when the window is closed. The program can't end until the GUI system is shut down. You have to call System.exit() to force the system to shut everything down and exit from the program.