Section 7.2
Array Processing
ARRAYS ARE THE MOST BASIC AND THE MOST IMPORTANT type of data structure, and techniques for processing arrays are among the most important programming techniques you can learn. Two fundamental array processing techniques -- searching and sorting -- will be covered in the next section. This section introduces some of the basic ideas of array processing in general.
In many cases, processing an array means applying the same operation to each item in the array. This is commonly done with a for loop. A loop for processing all the items in an array A has the form:
// do any necessary initialization
for (int i = 0; i < A.length; i++) {
. . . // process A[i]
}
Suppose, for example, that A is an array of type double[]. Suppose that the goal is to add up all the numbers in the array. An informal algorithm for doing this would be:
Start with 0;
Add A[0]; (process the first item in A)
Add A[1]; (process the second item in A)
.
.
.
Add A[ A.length - 1 ]; (process the last item in A)
Putting the obvious repetition into a loop and giving a name to the sum, this becomes:
double sum = 0; // start with 0
for (int i = 0; i < A.length; i++)
sum += A[i]; // add A[i] to the sum, for
// i = 0, 1, ..., A.length - 1
Note that the continuation condition, "i < A.length", implies that the last value of i that is actually processed is A.length-1, which is the index of the final item in the array. It's important to use "<" here, not "<=", since "<=" would give an array out of bounds error.
Eventually, you should almost be able to write loops similar to this one in your sleep. I will give a few more simple examples. Here is a loop that will count the number of items in the array A which are less than zero:
int count = 0; // start with 0 items counted
for (int i = 0; i < A.length; i++) {
if (A[i] < 0.0) // if this item is less than zero...
count++; // ...then count it
}
// At this point, the value of count is the number
// of items that have passed the test of being < 0
Replace the test "A[i] < 0.0", if you want to count the number of items in an array that satisfy some other property. Here is a variation on the same theme. Suppose you want to count the number of times that an item in the array A is equal to the item that follows it. The item that follows A[i] in the array is A[i+1], so the test in this case is "A[i] == A[i+1]". But there is a catch: This test cannot be applied when A[i] is the last item in the array, since then there is no such item as A[i+1]. The result of trying to apply the test in this case would be an array out of bounds error. This just means that we have to stop one item short of the final item:
int count = 0;
for (int i = 0; i < A.length - 1; i++) {
if (A[i] == A[i+1])
count++;
}
Another typical problem is to find the largest number in A. The strategy is to go through the array, keeping track of the largest number found so far. We'll store the largest number found so far in a variable called max. As we look through the array, whenever we find a number larger than the current value of max, we change the value of max to that larger value. After the whole array has been processed, max is the largest item in the array overall. The only question is, what should the original value of max be? It makes sense to start with max equal to A[0], and then to look through the rest of the array, starting from A[1], for larger items:
double max = A[0];
for (int i = 1; i < A.length; i++) {
if (A[i] > max)
max = A[i];
}
// at this point, max is the largest item in A
(There is one subtle problem here. It's possible in Java for an array to have length zero. In that case, A[0] doesn't exist, and the reference to A[0] in the first line gives an array out of bounds error. However, zero-length arrays are something that you want to avoid in real problems. Anyway, what would it mean to ask for the largest item in an array that contains no items at all?)
As a final example of basic array operations, consider the problem of copying an array. To make a copy of our sample array A, it is not sufficient to say
double[] B = A;
since this does not create a new array object. All it does is declare a new array variable and make it refer to the same object to which A refers. (So that, for example, a change to A[i] will automatically change B[i] as well.) To make a new array that is a copy of A, it is necessary to make a new array object and to copy each of the individual items from A into the new array:
double[] B = new double[A.length]; // make a new array object,
// the same size as A
for (int i = 0; i < A.length; i++)
B[i] = A[i]; // copy each item from A to B
Partially Full Arrays
Once an array object has been created, it has a fixed size. Often, though, the number of items that we want to store in an array changes as the program runs. Since the size of the array can't actually be changed, a separate counter variable must be used to keep track of how many spaces in the array are in use. (Of course, every space in the array has to contain something; the question is, how many spaces contain useful or valid items?)
Suppose, for example, that your program is a game, and that players can join the game and leave the game as it progresses. As a good object-oriented programmer, you would probably have a class named Player to represent each individual player in the game. A list of all players who are currently in the game could be stored in an array, playerList, of type Player[]. Since the number of players can change, you will also need a variable, playerCt, to record the number of players currently in the game. Assuming that there will never be more than 10 players in the game, you could declare the variables as:
Player[] playerList = new Player[10]; // up to 10 players
int playerCt = 0; // at the start, there are no players
After some players have joined the game, playerCt will be greater than 0, and the player objects representing the players will be stored in the array items playerList[0], playerList[1], ..., playerList[playerCt-1]. Note that the array item playerList[playerCt] is not in use. The procedure for adding a new player, newPlayer, to the game is simple:
playerList[playerCt] = newPlayer; // put new player in next
// available spot in array
playerCt++; // and increment playerCt to count the new player
There will be a problem, of course, if you try to add more than 10 players to the game. It's possible to allow an unlimited number of players if you are willing to create a new, larger array whenever you run out of space:
// add a new player, even if the current array is full
if (playerCt == playerList.length) { // test if array is full
Player[] temp = new Player[playerCt + 10]; // make a bigger array
for (int i = 0; i < playerCt; i++)
temp[i] = playerList[i]; // copy REFERENCES to player objects
playerList = temp; // set playerList to refer to new array
// (the old array will be garbage-collected)
}
// At this point, we know there is room in the array
playerList[playerCt] = newPlayer; // add the new player...
playerCt++; // ...and count it
Deleting a player from the game is a little harder, since you don't want to leave a "hole" in the array. Suppose you want to delete the player at index k in playerList. If you are not worried about keeping the players in any particular order, then one way to do this is to move the player from the last position in the array into position k and then to decrement the value of playerCt:
playerList[k] = playerList[playerCt - 1];
playerCt--;
It's worth emphasizing that the player example given above deals with an array whose base type is a class. An item in the array is either null or is a reference to an object belonging to the class Player. The Player objects themselves are not stored in the array. Note that because of the rules for assignment in Java, the objects can actually belong to subclasses of Player.
As another example, suppose that a class Shape represents the general idea of a shape drawn on a screen, and that it has subclasses to represent specific types of shapes such as lines, rectangles, rounded rectangles, ovals, filled-in ovals, and so forth. (Shape itself would be an abstract class, as discussed in Section 4.3.) Then an array of type Shape[] can be declared and can hold references to objects belonging to the subclasses of Shape. For example, the situation created by the statements
Shape[] shapes = new Shape[100]; // array to hold 100 shapes
shapes[0] = new Rect(); // put some objects in the array
shapes[1] = new Line(); // (A real program would
shapes[2] = new FilledOval(); // use some parameters here.)
int shapeCt = 3; // keep track of number of objects in array
could be illustrated as:
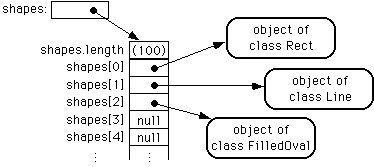
Such an array could be useful in a drawing program. The array could be used to hold a list of shapes to be displayed. If the Shape class includes a redraw() method for drawing the shape, then all the shapes in the array could be redrawn with a simple for loop:
for (int i = 0; i < shapeCt; i++)
shapes[i].redraw();
The statement "shapes[i].redraw();" calls the redraw() method belonging to the particular shape at index i in the array. Each object knows how to redraw itself, so that repeated executions of the statement can produce a variety of different shapes on the screen. This is nice example both of polymorphism and of array processing.