Section 7.4
Two-Dimensional Arrays
ANY TYPE CAN BE USED AS THE BASE TYPE FOR AN ARRAY. You can have an array of ints, an array of Strings, or an array of Objects... And, since an array type is a first-class Java type, you can, in particular, have an array of arrays. For example, an array of ints is said to have the type int[]. This means that there is automatically another type, int[][], which represents an "array of arrays of ints". Such an array is said to be a two-dimensional array. (Of course once you have the type int[][], there is nothing to stop you from forming the type int[][][], which represents a three-dimensional array -- and so on. However, in these notes I won't venture beyond the second dimension.)
The command "int[][] A = new int[3][4]" declares a variable, A, of type int[][], and it initializes that variable to refer to a newly created object. That object is an array of arrays of ints. The notation int[3][4] indicates that there are 3 arrays-of-ints in the array A, and that there are 4 ints in each of those arrays. However, trying to think in such terms can get a bit confusing -- as you might have already noticed. So it is customary to think of a two-dimensional array of items as a rectangular grid or matrix of items. The notation int[3][4] can then be taken to describe a grid of ints with 3 rows and 4 columns. The following picture might help:
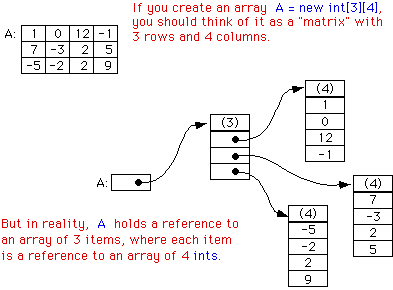
For the most part, you can ignore the reality and keep the picture of a grid in mind. Sometimes, though, you will need to remember that each row in the grid is really an array in itself. These rows can be referred to as A[0], A[1], and A[2]. Each row is in fact an array of type int[]. It could, for example, be passed to a subroutine that asks for a parameter of type int[].
You can pick out a particular item from a given row, such as A[1], by adding another index. For example, A[1][3] refers to item number 3 in row number 1. Keep in mind, of course, that both rows and columns are numbered starting from zero. So, in the above example, A[1][3] is 5. More generally, A[i][j] refers to the int in row number i and column number j. The 12 items in A would be named as follows:
A[0][0] A[0][1] A[0][2] A[0][3]
A[1][0] A[1][1] A[1][2] A[1][3]
A[2][0] A[2][1] A[2][2] A[2][3]
It might be worth noting that A.length gives the number of rows of A. To get the number of columns in A, you have to ask how many ints there are in a row; this number would be given by A[0].length, or equivalently by A[1].length or A[2].length. (There is actually no rule that says that the rows of an array must have the same length, and some advanced applications of arrays use varying-sized rows. But if you use the new operator to create an array in the manner described above, you'll get an array with equal-sized rows.)
It's possible to fill a two-dimensional array with specified items at the time it is created. Recall that when an ordinary one-dimensional array variable is declared, it can be assigned an "array initializer," which is just a list of values enclosed between braces, { and }. Similarly, a two-dimensional array can be created as a list of array initializers, one for each row in the array. For example, the array A shown in the picture above could be created with:
int[][] A = { { 1, 0, 12, -1 },
{ 7, -3, 2, 5 },
{ -5, -2, 2, 9 }
};
If no initializer is provided for an array, then when it is created it is automatically filled with the appropriate value: zero for numbers, false for boolean, and null for objects.
A two-dimensional array can be used whenever the data being represented can be naturally arranged into rows and columns. Often, the grid is built into the problem. For example, a chess board is a grid with 8 rows and 8 columns. If a class named ChessPiece is available to represent individual chess pieces, then the contents of a chess board could be represented by a two-dimensional array
ChessPiece[][] board = new ChessPiece[8][8];
Or consider the "mosaic" of colored squares used as an example in Section 3.6. The data about the color of each of the squares in the mosaic is stored in an array of type Color[][]. If the mosaic has ROWS rows and COLUMNS columns, then the array of color data can be created with the statement
Color[][] colorGrid = new Color[ROWS][COLUMNS];
When the color of the square in row i and column j is set to some color value c, the square is redrawn on the screen in the new color, and the color is stored in the array with an assignment "colorGrid[i][j] = c". The information in the colorGrid array can be used to redraw the whole mosaic when necessary. The information in the array is also used when you want to find out the color at a particular location in the array. The assignment statement "c = colorGrid[i][j]" gets the color of the square in row i and column j.
The grid is not always so visually obvious in a problem. Consider a company that owns 25 stores. Suppose that the company has data about the profit earned at each store for each month in the year 1998. If the stores are numbered from 0 to 24, and if the twelve months from January '98 through December '98 are numbered from 0 to 11, then the profit data could be stored in an array, profit, constructed as follows:
double[][] profit = new double[25][12];
profit[3][2] would be the amount of profit earned at store number 3 in March, and more generally, profit[storeNum][monthNum] would be the amount of profit earned in store number storeNum in month number month. In this example, the one-dimensional array profit[storeNum] has a very useful meaning: It is just the profit data for one particular store for the whole year.
Just as in the case of one-dimensional arrays, two-dimensional arrays are often processed using for statements. To process all the items in a two-dimensional array, you have to use one for statement nested inside another. If the array A is declared as
int[][] A = new int[3][4];
then you could store a zero into each location in A with:
for (int row = 0; row < 3; row++) {
for (int column = 0; column < 4; column++) {
A[row][column] = 0;
}
}
The first time the outer for loop executes (with row = 0), the inner for loop fills in the four values in the first row of A, namely A[0][0] = 0, A[0][1] = 0, A[0][2] = 0, and A[0][3] = 0. The next execution of the outer for loop fills in the second row of A. And the third and final execution of the outer loop fills in the final row of A.
Similarly, you could add up all the items in A with:
int sum = 0;
for (int i = 0; i < 3; i++)
for (int j = 0; j < 4; i++)
sum = sum + A[i][j];
If we did the same thing with the profit array discussed above, this example might seem a little more interesting. The sum would be the total profit earned by the company over the course of the entire year in all of its twenty-five stores.
This profit example demonstrates that sometimes it is necessary to process a single row or a single column of an array. For example, to compute the total profit earned by the company in December, that is, in month number 11, you could use the loop:
double decemberProfit = 0.0;
for (storeNum = 0; storeNum < 25; storeNum++)
decemberProfit += profit[storeNum][11];
We could extend this idea to create a one-dimensional array that contains the total profit for each month of the year:
double[] monthlyProfit = new double[12];
for (int month = 0; month < 12; month++) {
// compute the total profit from all stores in this month
monthlyProfit[month] = 0.0;
for (int store = 0; store < 25; store++)
monthlyProfit[month] += profit[store][month];
}
As a final example of processing two-dimensional arrays, suppose that we wanted to know which store generated the most profit over the course of the year. To do this, we have to add up the monthly profits for each store. In array terms, this means that we want to find the sum of each row in the array. As we do this, we want to keep track of which row produces the largest total.
double maxProfit; // maximum profit earned by a store
int bestStore; // the number of the store with the
// maximum profit
double total = 0.0; // total profit for one store;
// first compute the profit from store number 0
for (int month = 0; month < 12; month++)
total += profit[0][month];
bestStore = 0; // start by assuming that the best
maxProfit = total; // store is store number 0
// Now, go through the other stores, and whenever you
// find one with a bigger profit than maxProfit, revise
// the assumptions about bestStore and maxProfit
for (store = 1; store < 25; store++) {
total = 0.0;
for (month = 0; month < 12; month++)
total += profit[store][month];
if (total > maxProfit) {
maxProfit = total; // best profit seen so far!
bestStore = store; // and it came from this store
}
}
// At this point, maxProfit is the best profit of any
// of the 25 stores, and bestStore is a store that
// generated that profit. (Note that there could be
// other stores that generated the same profit.)