Section 8.5
Multi-Dimensional Arrays
ANY TYPE CAN BE USED AS THE BASE TYPE FOR AN ARRAY. You can have an array of ints, an array of Strings, an array of Objects, and so on. In particular, since an array type is a first-class Java type, you can have an array of arrays. For example, an array of ints has type int[]. This means that there is automatically another type, int[][], which represents an "array of arrays of ints". Such an array is said to be a two-dimensional array. Of course once you have the type int[][], there is nothing to stop you from forming the type int[][][], which represents a three-dimensional array -- and so on. There is no limit on the number of dimensions that an array type can have. However, arrays of dimension three or higher are fairly uncommon, and I concentrate here mainly on two-dimensional arrays. The type BaseType[][] is usually read "two-dimensional array of BaseType" or "BaseType array array".
The declaration statement "int[][] A;" declares a variable named A of type int[][]. This variable can hold a reference to an object of type int[][]. The assignment statement "A = new int[3][4];" creates a new two-dimensional array object and sets A to point to the newly created object. As usual, the declaration and assignment could be combined in a single declaration statement "int[][] A = new int[3][4];". The newly created object is an array of arrays-of-ints. The notation int[3][4] indicates that there are 3 arrays-of-ints in the array A, and that there are 4 ints in each array-of-ints. However, trying to think in such terms can get a bit confusing -- as you might have already noticed. So it is customary to think of a two-dimensional array of items as a rectangular grid or matrix of items. The notation "new int[3][4]" can then be taken to describe a grid of ints with 3 rows and 4 columns. The following picture might help:
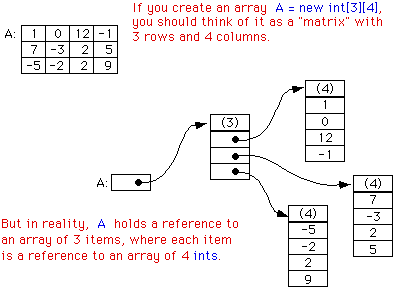
For the most part, you can ignore the reality and keep the picture of a grid in mind. Sometimes, though, you will need to remember that each row in the grid is really an array in itself. These arrays can be referred to as A[0], A[1], and A[2]. Each row is in fact a value of type int[]. It could, for example, be passed to a subroutine that asks for a parameter of type int[].
The notation A[1] refers to one of the rows of the array A. Since A[1] is itself an array of ints, You can another subscript to refer to one of the positions in that row. For example, A[1][3] refers to item number 3 in row number 1. Keep in mind, of course, that both rows and columns are numbered starting from zero. So, in the above example, A[1][3] is 5. More generally, A[i][j] refers to the grid position in row number i and column number j. The 12 items in A are named as follows:
A[0][0] A[0][1] A[0][2] A[0][3]
A[1][0] A[1][1] A[1][2] A[1][3]
A[2][0] A[2][1] A[2][2] A[2][3]
A[i][j] is actually a variable of type int. You can assign integer values to it or use it in any other context where an integer variable is allowed.
It might be worth noting that A.length gives the number of rows of A. To get the number of columns in A, you have to ask how many ints there are in a row; this number would be given by A[0].length, or equivalently by A[1].length or A[2].length. (There is actually no rule that says that all the rows of an array must have the same length, and some advanced applications of arrays use varying-sized rows. But if you use the new operator to create an array in the manner described above, you'll always get an array with equal-sized rows.)
Three-dimensional arrays are treated similarly. For example, a three-dimensional array of ints could be created with the declaration statement "int[][][] B = new int[7][5][11];". It's possible to visualize the value of B as a solid 7-by-5-by-11 block of cells. Each cell holds an int and represents one position in the three-dimensional array. Individual positions in the array can be referred with variable names of the form B[i][j][k]. Higher-dimensional arrays follow the same pattern, although for dimensions greater than three, there is no easy way to visualize the structure of the array.
It's possible to fill a multi-dimensional array with specified items at the time it is declared. Recall that when an ordinary one-dimensional array variable is declared, it can be assigned an "array initializer," which is just a list of values enclosed between braces, { and }. Array initializers can also be used when a multi-dimensional array is declared. An initializer for a two-dimensional array consists of a list of one-dimensional array initializers, one for each row in the two-dimensional array. For example, the array A shown in the picture above could be created with:
int[][] A = { { 1, 0, 12, -1 },
{ 7, -3, 2, 5 },
{ -5, -2, 2, 9 }
};
If no initializer is provided for an array, then when the array is created it is automatically filled with the appropriate value: zero for numbers, false for boolean, and null for objects.
Just as in the case of one-dimensional arrays, two-dimensional arrays are often processed using for statements. To process all the items in a two-dimensional array, you have to use one for statement nested inside another. If the array A is declared as
int[][] A = new int[3][4];
then you could store a zero into each location in A with:
for (int row = 0; row < 3; row++) {
for (int column = 0; column < 4; column++) {
A[row][column] = 0;
}
}
The first time the outer for loop executes (with row = 0), the inner for loop fills in the four values in the first row of A, namely A[0][0] = 0, A[0][1] = 0, A[0][2] = 0, and A[0][3] = 0. The next execution of the outer for loop fills in the second row of A. And the third and final execution of the outer loop fills in the final row of A.
Similarly, you could add up all the items in A with:
int sum = 0;
for (int i = 0; i < 3; i++)
for (int j = 0; j < 4; i++)
sum = sum + A[i][j];
To process a three-dimensional array, you would, of course, use triply nested for loops.
A two-dimensional array can be used whenever the data being represented can be naturally arranged into rows and columns. Often, the grid is built into the problem. For example, a chess board is a grid with 8 rows and 8 columns. If a class named ChessPiece is available to represent individual chess pieces, then the contents of a chess board could be represented by a two-dimensional array:
ChessPiece[][] board = new ChessPiece[8][8];
Or consider the "mosaic" of colored rectangles used as an example in Section 4.6. The mosaic is implemented by class named MosaicCanvas. The data about the color of each of the rectangles in the mosaic is stored in an instance variable named grid of type Color[][]. Each position in this grid is occupied by a value of type Color. There is one position in the grid for each colored rectangle in the mosaic. The actual two-dimensional array is created by the statement:
grid = new Color[ROWS][COLUMNS];
where ROWS is the number of rows of rectangles in the mosaic and COLUMNS is the number of columns. The value of the Color variable grid[i][j] is the color of the rectangle in row number i and column number j. When the color of that rectangle is changed to some color value, c, the value stored in grid[i][j] is changed with a statement of the form "grid[i][j] = c;". When the mosaic is redrawn, the values stored in the two-dimensional array are used to decide what color to make each rectangle. Here is a simplified version of the paint() method from the MosaicCanvas class, so you can see how it uses the array:
public void paint(Graphics g) {
// Draw all the colored rectangles in the grid.
int rowHeight = getSize().height / ROWS;
int colWidth = getSize().width / COLUMNS;
for (int row = 0; row < ROWS; row++) {
for (int col = 0; col < COLUMNS; col++) {
g.setColor( grid[row][col] ); // Get color from array.
g.fillRect( col*colWidth, row*rowHeight,
colWidth, rowHeight );
}
}
}
Sometimes two-dimensional arrays are used in problems in which the grid is not so visually obvious. Consider a company that owns 25 stores. Suppose that the company has data about the profit earned at each store for each month in the year 2000. If the stores are numbered from 0 to 24, and if the twelve months from January '00 through December '00 are numbered from 0 to 11, then the profit data could be stored in an array, profit, constructed as follows:
double[][] profit = new double[25][12];
profit[3][2] would be the amount of profit earned at store number 3 in March, and more generally, profit[storeNum][monthNum] would be the amount of profit earned in store number storeNum in month number monthNum. In this example, the one-dimensional array profit[storeNum] has a very useful meaning: It is just the profit data for one particular store for the whole year.
Let's assume that the profit array has already been filled with data. This data can be processed in a lot of interesting ways. For example, the total profit for the company -- for the whole year from all its stores -- can be calculated by adding up all the entries in the array:
double totalProfit; // Company's total profit in 2000.
totalProfit = 0;
for (int store = 0; store < 25; store++) {
for (int month = 0; month < 12; month++)
totalProfit += profit[store][month];
}
Sometimes it is necessary to process a single row or a single column of an array, not the entire array. For example, to compute the total profit earned by the company in December, that is, in month number 11, you could use the loop:
double decemberProfit = 0.0;
for (storeNum = 0; storeNum < 25; storeNum++)
decemberProfit += profit[storeNum][11];
Let's extend this idea to create a one-dimensional array that contains the total profit for each month of the year:
double[] monthlyProfit; // Holds profit for each month.
monthlyProfit = new double[12];
for (int month = 0; month < 12; month++) {
// compute the total profit from all stores in this month.
monthlyProfit[month] = 0.0;
for (int store = 0; store < 25; store++) {
// Add the profit from this store in this month
// into the total profit figure for the month.
monthlyProfit[month] += profit[store][month];
}
}
As a final example of processing the profit array, suppose that we wanted to know which store generated the most profit over the course of the year. To do this, we have to add up the monthly profits for each store. In array terms, this means that we want to find the sum of each row in the array. As we do this, we need to keep track of which row produces the largest total.
double maxProfit; // Maximum profit earned by a store.
int bestStore; // The number of the store with the
// maximum profit.
double total = 0.0; // Total profit for one store.
// First compute the profit from store number 0.
for (int month = 0; month < 12; month++)
total += profit[0][month];
bestStore = 0; // Start by assuming that the best
maxProfit = total; // store is store number 0.
// Now, go through the other stores, and whenever we
// find one with a bigger profit than maxProfit, revise
// the assumptions about bestStore and maxProfit.
for (store = 1; store < 25; store++) {
// Compute this store's profit for the year.
total = 0.0;
for (month = 0; month < 12; month++)
total += profit[store][month];
// Compare this store's profits with the highest
// profit we have seen among the preceding stores.
if (total > maxProfit) {
maxProfit = total; // Best profit seen so far!
bestStore = store; // It came from this store.
}
} // end for
// At this point, maxProfit is the best profit of any
// of the 25 stores, and bestStore is a store that
// generated that profit. (Note that there could also be
// other stores that generated exactly the same profit.)
For the rest of this section, we'll look at a more substantial example. Here is an applet that lets two users play checkers against each other. A player moves by clicking on the piece to be moved and then on the empty square to which it is to be moved. The squares that the current player can legally click are hilited. A piece that has been selected to be moved is surrounded by a white border. Other pieces that can legally be moved are surrounded by a cyan-colored border. If a piece has been selected, each empty square that it can legally move to is hilited with a green border. The game enforces the rule that if the current player can jump one of the opponent's pieces, then the player must jump. When a player's piece becomes a king, by reaching the opposite end of the board, a big white "K" is drawn on the piece.
I will only cover a part of the programming of this applet. I encourage you to read the complete source code, Checkers.java. At over 700 lines, this is a more substantial example than anything you've seen before in this course, but it's an excellent example of state-based, event-driven programming. The source file defines four classes. The logic of the game is implemented in a class named CheckersCanvas.
The data about the pieces on the board are stored in a two-dimensional array. Because of the complexity of the program, I wanted to divide it into several classes. One of these classes is CheckersData, which handles the data for the board. It is mainly this class that I want to talk about.
The CheckersData class has an instance variable named board of type int[][]. The value of board is set to "new int[8][8]", an 8-by-8 grid of integers. The values stored in the grid are defined as constants representing the possible contents of a square on a checkerboard:
public static final int
EMPTY = 0, // Value representing an empty square.
RED = 1, // A regular red piece.
RED_KING = 2, // A red king.
BLACK = 3, // A regular black piece.
BLACK_KING = 4; // A black king.
The constants RED and BLACK are also used in my program (or, perhaps, misused) to represent the two players in the game. When a game is started, the values in the variable, board, are set to represent the initial state of the board. The grid of values looks like
0 1 2 3 4 5 6 6
0 BLACK EMPTY BLACK EMPTY BLACK EMPTY BLACK EMPTY
1 EMPTY BLACK EMPTY BLACK EMPTY BLACK EMPTY BLACK
2 BLACK EMPTY BLACK EMPTY BLACK EMPTY BLACK EMPTY
3 EMPTY EMPTY EMPTY EMPTY EMPTY EMPTY EMPTY EMPTY
4 EMPTY EMPTY EMPTY EMPTY EMPTY EMPTY EMPTY EMPTY
5 EMPTY RED EMPTY RED EMPTY RED EMPTY RED
6 RED EMPTY RED EMPTY RED EMPTY RED EMPTY
7 EMPTY RED EMPTY RED EMPTY RED EMPTY RED
A black piece can only move "down" the grid. That is, the row number of the square it moves to must be greater than the row number of the square it comes from. A red piece can only move up the grid. Kings of either color, of course, can move in both directions.
One function of the CheckersData class is to take care of all the details of making moves on the board. An instance method named makeMove() is provided to do this. When a player moves a piece from one square to another, the values stored at two positions in the array are changed. But that's not all. If the move is a jump, then the piece that was jumped is removed from the board. (The method checks whether the move is a jump by checking if the square to which the piece is moving is two rows away from the square where it starts.) Furthermore, a RED piece that moves to row 0 or a BLACK piece that moves to row 7 becomes a king. This is good programming: the rest of the program doesn't have to worry about any of these details. It just calls this makeMove() method:
public void makeMove(int fromRow, int fromCol, int toRow, int toCol) {
// Make the move from (fromRow,fromCol) to (toRow,toCol). It is
// ASSUMED that this move is legal! If the move is a jump, the
// jumped piece is removed from the board. If a piece moves
// to the last row on the opponent's side of the board, the
// piece becomes a king.
board[toRow][toCol] = board[fromRow][fromCol]; // Move the piece.
board[fromRow][fromCol] = EMPTY;
if (fromRow - toRow == 2 || fromRow - toRow == -2) {
// The move is a jump. Remove the jumped piece from the board.
int jumpRow = (fromRow + toRow) / 2; // Row of the jumped piece.
int jumpCol = (fromCol + toCol) / 2; // Column of the jumped piece.
board[jumpRow][jumpCol] = EMPTY;
}
if (toRow == 0 && board[toRow][toCol] == RED)
board[toRow][toCol] = RED_KING; // Red piece becomes a king.
if (toRow == 7 && board[toRow][toCol] == BLACK)
board[toRow][toCol] = BLACK_KING; // Black piece becomes a king.
} // end makeMove()
An even more important function of the CheckersData class is to find legal moves on the board. In my program, a move in a Checkers game is represented by an object belonging to the following class:
class CheckersMove {
// A CheckersMove object represents a move in the game of
// Checkers. It holds the row and column of the piece that is
// to be moved and the row and column of the square to which
// it is to be moved. (This class makes no guarantee that
// the move is legal.)
int fromRow, fromCol; // Position of piece to be moved.
int toRow, toCol; // Square it is to move to.
CheckersMove(int r1, int c1, int r2, int c2) {
// Constructor. Set the values of the instance variables.
fromRow = r1;
fromCol = c1;
toRow = r2;
toCol = c2;
}
boolean isJump() {
// Test whether this move is a jump. It is assumed that
// the move is legal. In a jump, the piece moves two
// rows. (In a regular move, it only moves one row.)
return (fromRow - toRow == 2 || fromRow - toRow == -2);
}
} // end class CheckersMove.
The CheckersData class has an instance method which finds every legal moves that is currently available for a specified player. This method is a function that returns an array of type CheckersMove[]. The array contains all the legal moves, represented as CheckersMove objects. The specification for this method reads
public CheckersMove[] getLegalMoves(int player)
// Return an array containing all the legal CheckersMoves
// for the specified player on the current board. If the player
// has no legal moves, null is returned. The value of player
// should be one of the constants RED or BLACK; if not, null
// is returned. If the returned value is non-null, it consists
// entirely of jump moves or entirely of regular moves, since
// if the player can jump, only jumps are legal moves.
A brief pseudocode algorithm for the method is
Start with an empty list of moves
Find any legal jumps and add them to the list
if there are no jumps:
Find any other legal moves and add them to the list
if the list is empty:
return null
else:
return the list
Now, what is this "list"? We have to return the legal moves in an array. But since an array has a fixed size, we can't create the array until we know how many moves there are, and we don't know that until near the end of the method, after we've already made the list! A neat solution is to use a Vector instead of an array to hold the moves as we find them. As we add moves to the vector, it will grow just as large as necessary. At the end of the method, we can create the array that we really want and copy the data into it:
Let "moves" be an empty vector
Find any legal jumps and add them to moves
if moves.size() is 0:
Find any other legal moves and add them to moves
if moves.size() is 0:
return null
else:
Let moveArray be an array of CheckersMoves of length moves.size()
Copy the contents of moves into moveArray
return moveArray
Now, how do we find the legal jumps or the legal moves? The information we need is in the board array, but it takes some work to extract it. We have to look through all the positions in the array and find the pieces that belong to the current player. For each piece, we have to check each square that it could conceivably move to, and check whether that would be a legal move. There are four squares to consider. For a jump, we want to look at squares that are two rows and two columns away from the piece. Thus, the line in the algorithm that says "Find any legal jumps and add them to moves" expands to:
For each row of the board:
For each column of the board:
if one of the player's pieces is at this location:
if it is legal to jump to row + 2, column + 2
add this move to moves
if it is legal to jump to row - 2, column + 2
add this move to moves
if it is legal to jump to row + 2, column - 2
add this move to moves
if it is legal to jump to row - 2, column - 2
add this move to moves
The line that says "Find any other legal moves and add them to moves" expands to something similar, except that we have to look at the four squares that are one column and one row away from the piece. Testing whether a player can legally move from one given square to another given square is itself non-trivial. The square the player is moving to must actually be on the board, and it must be empty. Furthermore, regular red and black pieces can only move in one direction. I wrote the following utility method to check whether a player can make a given non-jump move:
private boolean canMove(int player, int r1, int c1, int r2, int c2) {
// This is called by the getLegalMoves() method to determine
// whether the player can legally move from (r1,c1) to (r2,c2).
// It is ASSUMED that (r1,c1) contains one of the player's
// pieces and that (r2,c2) is a neighboring square.
if (r2 < 0 || r2 >= 8 || c2 < 0 || c2 >= 8)
return false; // (r2,c2) is off the board.
if (board[r2][c2] != EMPTY)
return false; // (r2,c2) already contains a piece.
if (player == RED) {
if (board[r1][c1] == RED && r2 > r1)
return false; // Regular red piece can only move down.
return true; // The move is legal.
}
else {
if (board[r1][c1] == BLACK && r2 < r1)
return false; // Regular black piece can only move up.
return true; // The move is legal.
}
} // end canMove()
This method is called by my getLegalMoves() method to check whether one of the possible moves that it has found is actually legal. I have a similar method that is called to check whether a jump is legal. In this case, I pass to the method the square containing the player's piece, the square that the player might move to, and the square between those two, which the player would be jumping over. The square that is being jumped must contain one of the opponent's pieces. This method has the specification:
private boolean canJump(int player, int r1, int c1,
int r2, int c2, int r3, int c3) {
// This is called by two previous methods to check
// whether the player can legally jump from (r1,c1) to (r3,c3).
// It is assumed that the player has a piece at (r1,c1), that
// (r3,c3) is a position that is 2 rows and 2 columns distant
// from (r1,c1) and that (r2,c2) is the square between (r1,c1)
// and (r3,c3).
Given all this, you should be in a position to understand the complete getLegalMoves() method. It's a nice way to finish off this chapter, since it combines several topics that we've looked at: one-dimensional arrays, vectors, and two-dimensional arrays:
public CheckersMove[] getLegalMoves(int player) {
if (player != RED && player != BLACK)
return null;
int playerKing; // The constant for a King belonging to the player.
if (player == RED)
playerKing = RED_KING;
else
playerKing = BLACK_KING;
Vector moves = new Vector(); // Moves will be stored in this vector.
/* First, check for any possible jumps. Look at each square on
the board. If that square contains one of the player's pieces,
look at a possible jump in each of the four directions from that
square. If there is a legal jump in that direction, put it in
the moves vector.
*/
for (int row = 0; row < 8; row++) {
for (int col = 0; col < 8; col++) {
if (board[row][col] == player || board[row][col] == playerKing) {
if (canJump(player, row, col, row+1, col+1, row+2, col+2))
moves.addElement(new CheckersMove(row, col, row+2, col+2));
if (canJump(player, row, col, row-1, col+1, row-2, col+2))
moves.addElement(new CheckersMove(row, col, row-2, col+2));
if (canJump(player, row, col, row+1, col-1, row+2, col-2))
moves.addElement(new CheckersMove(row, col, row+2, col-2));
if (canJump(player, row, col, row-1, col-1, row-2, col-2))
moves.addElement(new CheckersMove(row, col, row-2, col-2));
}
}
}
/* If any jump moves were found, then the user must jump, so we
don't add any regular moves. However, if no jumps were found,
check for any legal regular moves. Look at each square on
the board. If that square contains one of the player's pieces,
look at a possible move in each of the four directions from
that square. If there is a legal move in that direction,
put it in the moves vector.
*/
if (moves.size() == 0) {
for (int row = 0; row < 8; row++) {
for (int col = 0; col < 8; col++) {
if (board[row][col] == player
|| board[row][col] == playerKing) {
if (canMove(player,row,col,row+1,col+1))
moves.addElement(new CheckersMove(row,col,row+1,col+1));
if (canMove(player,row,col,row-1,col+1))
moves.addElement(new CheckersMove(row,col,row-1,col+1));
if (canMove(player,row,col,row+1,col-1))
moves.addElement(new CheckersMove(row,col,row+1,col-1));
if (canMove(player,row,col,row-1,col-1))
moves.addElement(new CheckersMove(row,col,row-1,col-1));
}
}
}
}
/* If no legal moves have been found, return null. Otherwise, create
an array just big enough to hold all the legal moves, copy the
legal moves from the vector into the array, and return the array.
*/
if (moves.size() == 0)
return null;
else {
CheckersMove[] moveArray = new CheckersMove[moves.size()];
for (int i = 0; i < moves.size(); i++)
moveArray[i] = (CheckersMove)moves.elementAt(i);
return moveArray;
}
} // end getLegalMoves