CPSC 124 (Winter 1998): Lab 8
Two-dimensional Arrays (and More)

FOR THE EIGHTH LAB in Computer Science 124, you'll be doing some more work with arrays. In the first exercise, you'll use a two-dimensional array to store playing cards. In the third exercise, you'll "debug" a program that is supposed to find prime numbers, but that doesn't quite work. The second exercise is not related to arrays, but it makes pretty pictures. Both the first and second exercise are meant partly to introduce ideas and techniques that you might be able to use in your final programming project.

This lab consists of three exercises which use three folders from the cpsc124 folder on the network: "Cards Applet Starter," "KaleidaSketch Starter," and "Buggy Prime Starter." You should copy these into your java folder on the M drive, and use the copies in the lab.

The exercises at the end of the lab are due in class on the Monday following the lab.

Outline of the Lab

A Two-Dimensional Array

Here's a very simple solitaire game: Deal cards from a deck of playing cards one at a time. As each card is dealt, you have to decide where to place it on a playing board. The board has spaces for 25 cards, arranged into a grid with five rows and five columns. Once you play a card, you can't move it and you can't cover it with another card. The game ends when you have filled the 25 spaces with 25 cards. The goal is to end the game with as good a Poker hand in each row and in each column. (Don't worry if you don't know about Poker -- it's not necessary to understand it to do the exercise.)

You can play the game in an applet on a separate page. (But don't think too long about it during the lab!) Note that if you try to place a card in a space that is already occupied, the applet won't do it. Try filling all 25 spots, and see what happens. You can also check that if you cover up the applet with another window, the applet will redraw itself correctly when you uncover it.

The "Cards Applet Folder" contains an incomplete version of the applet. (You can also read it here, along with the supporting files Card.java and Deck.java.) The game works, sort of, but: the user can replace one card on the board with another card; the applet can't properly redraw the cards on the board; and the game doesn't end after 25 cards have been played. The first two problems can be fixed by using a two-dimensional array of Cards to store the cards that are on the board. The second can be fixed by adding a counter that counts the number of cards that have been played so far. You assignment is to make these improvements to the applet. You just have to declare two instance variables and modify the startGame(), playCard(), and paint() methods. (In the paint method, you only need to modify the first few lines.)

For your two-dimensional array, you can declare a variable:

Card[][] cardGrid = new Card[5][5];

In the startGame() method, this array should be filled with null's to indicate that no cards have yet been played. In the playCard() method, when a card is added to the board, it should also be added to the array. In the paint() method, when the board is redrawn, the putCard() method should be called to display each card on the board.

The method used in this applet to draw individual cards uses some tricks that you have to ask about if you are interested.

By the way, thanks to Zach Brusko, who provided the card images that are used in this applet.

Sketching With Symmetry

To begin the second lab exercise, open the folder "KaleidaSketch Starter" and double-click on the .dsw file. When you run the program, you'll see a simple sketching applet that lets the user sketch curves by dragging the mouse. The user can select the color of the curve from a pop-up menu. The user can also clear the drawing area by filling it with solid black or solid white. Most of the work for this applet is already done, but one feature is unimplemented. There is a checkbox labeled "kaleidascopic." When this box is checked, the user should be able to sketch symmetric, kaleidascopic curves. To see what this is like, check out the finished applet, which is available on a separate page.

Your assignment for this exercise is to implement the kaleidascopic drawing feature. This is easier than it might sound. Suppose the user moves the mouse from a point (x1,y1) to a point (x2,y2). Currently, the applet just draws a line from (x1,y1) to (x2,y2). To get the kaleidascopic effect you also have to draw the other seven lines that can be obtained from this original line by horizontal, vertical, and diagonal reflection. This just takes a little math. Let's say that the width of the drawing area is w and that its height is h. This picture shows how seven additional points can be obtained as reflections of a point (a,b):

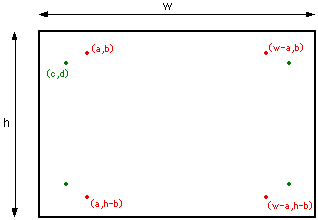
Reflections of the point (a,b)

The horizontal and vertical reflections of (a,b) are labeled. The diagonal reflection of (a,b) is labeled as (c,d). If the canvas were a square, (c,d) would just be equal to (b,a). However, because the canvas is not necessarily square, c and d should be defined as:

               c = (w * b) / h;
               d = (h * a) / w;

To get the remaining three points, take the horizontal and vertical reflections of (c,d). Note that each of the endpoints of the line, (x1,y1) and (x2,y2), must be reflected in this way to get the endpoints of the reflected lines.

You can do all your work in one method in the file KSCanvas.java. The following doDrawLine() method currently draws a single line from (x1,y1) to (x2,y2). But if the boolean instance variable, kaleidascopic, is true, then it is also supposed to draw the seven reflections of that line. You just have to add some commands to this method to draw the extra seven lines, if kaleidascopic is true:

           void doDrawLine(int x1, int y1, int x2, int y2) {
                 // User has dragged mouse from (x1,y1) to (x2,y2).  If kaleidascopic
                 // is false, this just draws a line from (x1,y1) to (x2,y2).  If
                 // kaleidascopic is false, it draws that line plus all its horizontal,
                 // vertical, and diagonal reflections.
              basicPutLine(x1,y1,x2,y2);
           }

This is a relatively short exercise that has to do mostly with understanding coordinates and doing some calculations. But you should take a look at the rest of the files KSCanvas.java and KaleidaSketch.java. (You can also read them here and here.) These files demonstrate several techniques that you might want to use in your final programming project:

Debugging

In class, we discussed finding prime numbers as an example of using arrays. The "Buggy Prime Finder" folder contains a version of the program that we discussed. However, this version of the program contains some bugs. (You can also read the buggy program here.)

A bug is an error in a program that causes it to crash or to give incorrect results when it is run. A bug is a semantic error rather than a syntax error. A syntax error would be found by the computer when you compile the program. A bug is much worse, since the computer can't find it for you. You have to debug the program yourself.

Your assignment for the third exercise of the lab is to debug the buggy prime-finder program.

If you run the program as it stands, it will just give you an empty window and sit there. The program has either crashed or gone into an infinite loop. (By the way, this shows the importance of testing the program for a small number of primes. The program is set to find 20 primes. If it were set to find 1000000 the first time you ran it, you'd probably think the program was still computing.) You have to figure out what is wrong and fix it. If you have sharp eyes, you might be able to find the problem by reading the program. Or you can try executing it by hand to see if you can find the problem that way. Let's say that none of this works. In that case, you have to do some debugging.

You have two choices about how to do the debugging. Your first choice is the traditional approach: Add some extra output statements to the program to print out intermediate results or other information that can help you determine the part of the program that is causing the problem. Any output statement in a loop will quickly expose an infinite loop. An output statement at the beginning of a subroutine can be used to make sure that it is being called properly, with the expected parameters. An output statement at the end of the subroutine will tell you whether it has completed its work properly.

The second debugging method is to use the debugger that is built into Developer Studio. The debugger let's you stop the program at any point to inspect the values of the program's variables. You can also step through the program one line at at time. Unfortunately, the debugger is itself a large and complex program that is not very easy to learn. Here is one way to use it: Click the mouse on the program to get a blinking cursor in the line where you would like to program to be stopped. Then, in the "Start Debug" submenu of the "Build" menu, choose the "Run to Cursor" command. The computer will start executing the program and will stop when it gets to the line containing the cursor. (You'll find that the program runs quite a bit more slowly with the debugger than without it.) The program's variables will be displayed in a window next to the program itself.

While the debugger is active, the "Build" menu is replaced by a "Debug" menu, which contains commands that you can use to control the execution of your program. The most useful are "Step Over," which executes one line in the program; "Run to Cursor," which continues execution until the computer gets to the line containing the blinking cursor; and "Restart," which starts executing the program again from the beginning. When you use the "Step Over" command on a subroutine call, the entire subroutine is executed in a single step. If you want to see what happens inside the subroutine, use the "Step Into" command instead.

Once you've found the error and get the programming running, you'll see that there is another problem with the program. It gives incorrect results. You should find and fix that problem as well.

Exercises to Turn in

Exercise 1. Turn in a printout of the CardsApplet.java file that you modified for the first lab exercise, above.

Exercise 2. Turn in a modified copy of SketchCanvas.java, showing the work you did for the second lab exercise, above. (Better yet, just turn in a copy of the new doDrawLine() method that you create.) Also, post a copy of your applet on the web and tell me its URL.

If you want to try for extra credit, consider adding another pop-up menu to the applet to control the types of symmetry that are applied. For example, you might provide a choice of two-way horizontal symmetry, two-way vertical symmetry, two-way diagonal symmetry, four-way horizontal/vertical symmetry or full eight-way symmetry. Drawing with different forms of symmetry is just a matter of deciding which of the eight possible reflected lines are drawn.

Exercise 3. Write an essay discussing the errors that you found in the buggy PrimeFinder program, above, and explaining how you found them. Also, use the fixed program to find the 100,000-th prime number and tell me what it is.

[ Lab Index | Online Notes ]