CPSC 225, Spring 2002
Second Test, April 5
This is the second test in CPSC 225: Intermediate Programming.
Question 1: What is a Binary Sort Tree ? How do they differ from other binary trees, and why are they useful?
Answer: A Binary Sort Tree is a binary tree that has the property that an inorder traversal of the tree will list the items in non-decreasing order. (Another way of saying this is that the tree has the Binary Sort Tree Property: For every node, all the items in the left subtree of that node are less than or equal to the item in the node, and all the items in the right subtree are greater than the item in the node.) Binary Sort Trees are useful because it is very efficient to search for an item.
Question 2: A recursive function should have at least one base case. What is meant by a base case of a recursion, and why are they so important? Give an example.
Answer: A base case of a recursive function is a case that can be handled directly, without calling the function recursively. It is important that every recursion have a base case, since otherwise it will never end. If a recursive function calls itself in all cases, the result is infinite recursion. As an example, when processing a binary tree recursively, the base case is usually the case where the tree is NULL (as, for example, in the function in Problem 10.)
Question 3: A bored programmer writes the following code and finds that the output consists of the numbers 42, 17, and 8049910. Explain how this output could occur. (Actual output can vary on different systems.)
int a;
int b;
int* p;
p = &a;
*p = 42;
p++;
*p = 17;
cout << a << endl;
cout << b << endl;
cout << p << endl;
Answer: The command "p = &a;" makes the pointer p point to a. (That is, the value of p is the address of a.) The command "*p = 42;" stores 42 in the memory location that p points to. Since p is pointing to a, this sets a to 42, so that when a is printed out, the value is 42. The command "p++;" makes p point to the next int in memory. (It actually just adds 4 to the value of p, since each int occupies 4 bytes of memory.) The result of doing this when p points to a variable is undefined. However, in this case it seems that b is stored directly after a in memory, so that the command "*p = 17;" sets b to 17. We can guess that this is true since when b is output, the value is 17. (Note: On our compiler, this worked for me when a and b were global variables, but not when they were local variables in main(). The compiler can put variables wherever it wants.) Finally, the last line outputs the value of p. The value of a pointer variable is the address of the memory location that it is pointing to. In this case, p is pointing to b, so that 8049910 is presumably the address of b. (Note: On our system, the actual output was "0x8049910". The "0x" indicates that this is actually a hexadecimal number.)
Question 4: When using C++ pointers, it is easy to make errors that can crash a program, or worse. Briefly describe two different errors of this type and the problems that might result.
Answer: There are several possible answers, including
- When memory is allocated with the "new" operator, failure to delete that memory when it is no longer needed can result in running out of memory and crashing the program, even though most of the memory is not actually being used for anything. (This is called a memory leak.)
- If p is a pointer that has not been initialized, then it might actually point to a part of memory that has not been given to the program. In this case, a reference to *p will crash the program. (This is called a segmentation fault in our version of g++. It means that you are trying to use memory that is outside the "segment" of memory allocated to your program.)
- Trying to delete memory that has already been deleted is an error that can have unpredictable results.
- Trying to refer to memory that has been deleted is an error that can have unpredictable results.
Question 5: Suppose that the following type is used to implement linked lists, as usual:
struct ListNode {
string item;
ListNode *next;
}
Suppose that head is a variable of type ListNode and that head points to the first node in a non-empty list. Write a program segment that will add the word "Fred" onto the end of the list. That is, it should be added to the list after what is currently the last node. (First, you have to find the last node...)
Answer:
ListNode *runner; // A pointer to "run" down the list.
while (runner->next != NULL) {
runner = runner->next;
}
// At this point, runner->next is NULL, so runner is pointing
// to the last node in the list. We just have to make a new
// node and attach it to this node by setting runner->next
// to point to it.
ListNode *newNode;
newNode = new ListNode;
newNode->item = "Fred";
newNode->next = NULL; // This is necessary so that the end of
// the list is properly marked!
runner->next = newNode;
Question 6: The class FullName, shown below, is used to store people's first and last names. Suppose that you want to be able to compare two FullName variables using the < operator (where A<B if A.last < B.last or if A.last == B.last and A.first < B.first. Write a definition that will overload < to make this possible.
Answer:
bool operator<(const FullName &A, const FullName &B) {
if ( A.last < B.last )
return true;
else if ( A.last == B.last && A.first < B.first )
return true;
else
return false;
}
Question 7: Complete the definition of the following recursive function. It should set a group of 1's in the grid to 0. That is, if grid[r][c] is 1, then it is set to 0, along with any other 1's that can be reached from position (r,c) by horizontal and/or vertical moves.
void makeOnesZero( int grid[100][100], int r, int c ) {
if ( r < 0 || r >= 100 || c < 0 || c >= 100 )
return; // Outside the grid -- don't do anything
Answer:
void makeOnesZero( int grid[100][100], int r, int c ) {
if ( r < 0 || r >= 100 || c < 0 || c >= 100 )
return; // Outside the grid -- don't do anything
if ( grid[r][c] == 1 ) {
// Make this spot 0 and make any 1's connected
// to it 0 by calling makeOnesZero recursively
// for the four neighboring squares.
grid[r][c] = 0; // (Do this FIRST to avoid infinite recursion.)
makeOnesZero(grid, r+1, c);
makeOnesZero(grid, r-1, c);
makeOnesZero(grid, r, c+1);
makeOnesZero(grid, r, c-1);
}
}
Question 8:
Suppose that a binary tree has the structure shown at
the right. Each node contains a single letter. When the
contents of the nodes are output using a postorder traversal
of the tree, the result is:
A B C D E F G H I J
Fill in the nodes in the tree at the right, so that a postorder traversal will produce this output.
Answer:
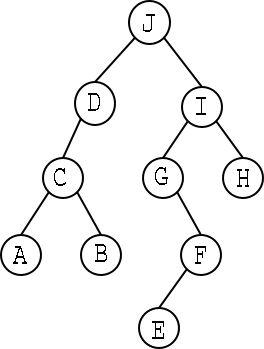
Question 9: Assume that the following type is defined and used to implement binary trees:
struct TreeNode {
int item;
TreeNode *left;
TreeNode *right;
}
Write a complete function that can be used to count the number of nodes in a tree (and return the answer).
Answer:
int countTreeNodes( TreeNode *root ) {
if (root == NULL) {
// An empty tree has no nodes, so return 0.
return 0;
}
else {
// For a non-empty tree, count the number of
// nodes in the left subtree and in the right
// subtree, and add 1 to the total in order to
// count the root node itself.
return countTreeNodes( root->left )
+ count TreeNodes( root->right )
+ 1 ;
}
}
Question 10: Assume that the type TreeNode is defined as in the previous problem. What does the following function do? Why?
TreeNode* mircp(TreeNode* root) {
if (root == NULL)
return NULL;
else {
TreeNode* m = new TreeNode;
m->item = root->item;
m->left = mircp(root->right);
m->right = mircp(root->left);
return m;
}
}
Answer: This function builds a "mirror copy" of a tree, and returns a pointer to the copy. That is, the return value is a pointer to a tree that is a copy of the original, except that all the nodes in the tree are reversed left-to-right. It is important to note that the reversal takes place on all levels of the tree. When m is created as the root of the new tree, it contains the same item as the root node of the original. However, the left subtree of m is a mirror-reversed copy of the right subtree from the original, and the right subtree of m is a reversed copy of the left subtree of the original.