In this lab, you will be working with recursion. In the first part of the lab, you will write a program that generates random sentences based on a set of syntax rules. In the second, you will use recursion to create pictures of fractals.
The grammar of natural languages such as English exhibits a recursive structure. This structure can be expressed in syntax rules written in the format known as BNF (Bachus-Naur Form, named after the people who invented it). You have proably seen BNF used to specify the syntax of programming languages. While BNF is ordinarily used as a guide for parsing (that is, determining whether and how a given string follows the syntax rules), it can also be used a a guide for generating strings that follow the syntax rules. An example of this can be found in the sample program SimpleRandomSentences. In this example, each syntax rule -- except for the most basic ones -- is represented by a method that generates strings that follow that rule. Where one syntax rule refers to another rule, the method that represents the first rule calls the method that represents the second rule.
For the first exercise of the lab, you should write a similar program that implements the following rules:
<sentence> ::= <simple_sentence> [ <conjunction> <sentence> ]
<simple_sentence> ::= <noun_phrase> <verb_phrase>
<noun_phrase> ::= <proper_noun> |
<determiner> [ <adjective> ]... <common_noun> [ who <verb_phrase> ]
<verb_phrase> ::= <intransitive_verb> |
<transitive_verb> <noun_phrase> |
is <adjective> |
believes that <simple_sentence>
<conjunction> ::= and | or | but | because
<proper_noun> ::= Fred | Jane | Richard Nixon | Miss America
<common_noun> ::= man | woman | fish | elephant | unicorn
<determiner> ::= a | the | every | some
<adjective> ::= big | tiny | pretty | bald
<intransitive_verb> ::= runs | jumps | talks | sleeps
<transitive_verb> ::= loves | hates | sees | knows | looks for | finds
As in SimpleRandomSentences.java, you can use arrays to implement the last seven rules in this list. (You might improve on that program by writing a single method "void String randomItem(String[] listOfStrings)" for picking a random item from an array of strings.) You are welcome to add to or modify the items in the lists given here.
For each of the first three rules, you should write a subroutine to represent that rule. Note that a choice of alternatives (represented in the rules by "|") can be implemented using a switch or if..else statement; the various choices don't necessarily have to have the same probability. An optional element (represented by brackets, "[ xxx ]") can be implemented by a simple if. And a repeated optional element (represented by brackets with dots, "[ xxx ]...") can be represented by a while loop. You should implement the first four rules exactly as stated here. The main routine should call the <sentence> subroutine to generate random sentences.
You have to be careful in this program to avoid infinite recursion in this program. Since it will use random choices, there is no guarantee that the recursion will ever end. If your probabilities of doing recursion and continuing loops are too high, it is possible for the program to get lost in recursive calls forever -- or to produce some finite but ridiculously long sentences. You should adjust your probabilities to make sure that this doesn't happen, but that you still get some interesting sentences.
A "fractal" is a geometric figure that has some kind of "self-similarity." In one type of fractal, the self-similarity is an exact recursive structure: The figure is made up of several pieces that are scaled-down copies of itself. For a true fractal, the recursion is infinite; each scaled-down copy is itself made up of smaller copies, which are made up of even smaller copies, and so on forever. On the computer screen, we can get good approximations of fractals by limiting the recursion to a finite level.

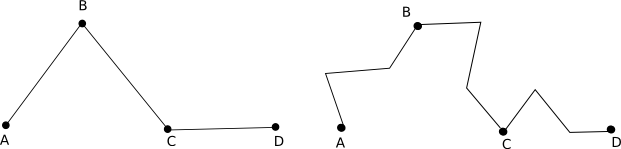
One way to produce such fractals is to start with a piecewise linear path from a point A to a point B, like the one shown on the left above. To form a fractal, take the path and replace each line segment in the path with a scaled-down copy of the original path. Then do the same thing to the new path -- replace each line segment with a scaled copy of the original path. By repeating this process to infinity, you get a true fractal. By repeating it for a finite number of steps, you get an approximation to a fractal. In the above figure, the path shown on the right is what you get when you apply just one step in the process to the path shown on the left.
If you follow the description I just gave, it can be hard to draw the path. It's easier if you use recursion (although there is still some rather complicated math). The idea is that we start with the original path, given as a sequence of points. This path is a "template" for the recursive paths that we will actually draw. The algorithm tells how to use the template to draw a path between any two points. The level of recursion that we want is also a parameter to the algorithm:
Algorithm "Recursive Walk", based on a path P = (s0,t0), (s1,t1), (s2,t2), ..., (sk-1,tk-1):
To go from a point (a1,b1) to a point (a2,b2), with recursion level n:
if n is 0:
go directly from (a1,b1) to (a2,b2) in a straight line
else:
find a transformed copy of the path P that goes from (a1,b1) to (a2,b2),
where the points on the copy are (x0,y0), (x1,y1), (x2,y2), ... (xk-1,yk-1)
with (x0,y0) = (a1,b1) and (xk-1,yk-1) = (a2,b2)
for (i = 1; i < k; i++):
call the algorithm recursively to go from (xi-1, yi-1) to (xi, yi) with recursion level n-1
The hard part of this algorithm is transforming the path P. It's easiest if we assume that P goes from the point (s0,t0) = (0,0) to the point (sk-1,tk-1) = (0,1). In that case, the points of the transformed path can be computed using the formulas:
xi = a1 + si*(a2-a1) - ti*(b2-b1)
yi = b1 + ti*(a2-a1) + si*(b2-b1)
Unfortunately, the original path is not likely to be given as a path from (0,0) to (1,0), so the data that you get for the path has to be transformed to make this true. Here is the actual code from my program that takes the original path given as an array of points (with integer coordinates) and transforms that data to get arrays s and t of type double that represent the path from (0,0) to (1,0):
private double[] s;
private double[] t;
public void setPoints(Point[] points) {
x1 = points[0].x;
y1 = points[0].y;
x2 = points[points.length-1].x;
y2 = points[points.length-1].y;
s = new double[points.length];
t = new double[points.length];
s[0] = t[0] = 0;
double d = (x2-x1)*(x2-x1) + (y2-y1)*(y2-y1);
for (int i = 1; i < points.length; i++) {
s[i] = ( (x2-x1)*(points[i].x-x1) + (y2-y1)*(points[i].y-y1)) / d;
t[i] = ( (x2-x1)*(points[i].y-y1) - (y2-y1)*(points[i].x-x1)) / d;
}
repaint();
}
The actual program that you will write is an interactive program where the user can drag points on the screen to create the original path that is used as the basis of the recursion. An executable jar file for the program can be found in the file /classes/s09/cs225/FunnyFractals.jar. The source code for the main program is in the file /classes/s09/cs225/FamousFractals.java; you will want to copy this file into your Eclipse project. You will have to create two classes, InputCanvas and DisplayCanvas. The main program and the executable program can serve as a guide for what needs to be in these classes. Each class can be written as a subclass of JPanel. Both classes need paintComponent methods to draw the contents of the panel. InputCanvas needs a mouse listener and mouse motion listener to allow the user to drag the points. As the user drags a point, you need to call repaint, and you need to call the setPoints method in the DisplayCanvas to get the new list of points into that class as well.
This assigment is obviously about more than recursion. It's also a chance for you to review (or learn) some GUI programming. You will probably need help on this one, and the due date for the second part of the lab will almost certainly be later than next Tuesday.