About The Turtle

The file TurtlePanel.java defines a panel that represents the turtle habitat. The habitat has x-coordinates that range from -10 on the left to 10 on the right, and it has y-coordinates that range from -10 on the bottom to 10 at the top. The turtle starts out in the center, at (0,0), facing to the right. The turtle has a "pen" that can be raised or lowered. If the pen is down when the turtle moves, it leaves a trail: The pen draws a line from the starting point to the point to which the turtle moves.

If turtle is a variable of type TurtlePanel, you give commands to the turtle by calling instance methods of turtle such as turtle.forward(5), turtle.turn(45), and turtle.penUp(). To learn about all the available methods, read the source code file, TurtlePanel.java.

The file TurteGraphics.java contains the main() routine. Currently, it draws a Sierpinski Triangle as an example. We looked at this example in class on Wednesday. You can run the program to see what it does.

TurtleGraphics.java includes a method delay(t) that causes the program to pause for t milliseconds when it is called. You can use this method to insert a delay into your program, to give the user a better chance to see what is going on.

Before you start working on the lab exercises, you might want to try some non-recursive turtle graphics to get more familiar with the concept. For example, try replacing the call to runSierpinskiDemo() at the end of main() with the following code, which is similar to an example that we looked at in class:

turtle.setTurtleIsVisible(false);
for (int i = 0; i < 180; i++) {
    for (int j = 0; j < 4; j++) {
        turtle.forward(7);
        turtle.turn(90);
    }
    turtle.turn(2);
    delay(50);
}

Recursive Drawing

For your exercises in recursive drawing, you will work entirely in the file TurtleGraphics.java (or in copies of that file). You will be writing at least four recursive methods. To show your work to the user, I suggest that you program a kind of slide show that shows the user all of your drawings, one after the other. To do this, you could put code such as the following at the end of main():

runExercise1();   // (but use better names!!!)
delay(4000);
runExercise2();
delay(4000);
runExercise3();
delay(4000);
runExercise4();

(If you don't like this idea, you can make several copies of TurtleGraphics.java and do one exercise in each copy.)

---

For the first exercise, you should implement the Koch curve, which we looked at in class as an example. You should write a method

   private static void koch( double size, int level )

to draw a Koch curve with a given size and level of recursion. Recall that a true Koch curve is a "fractal" which is made up of 4 smaller sized copies of itself. You can't draw a true Koch curve, but you can draw an approximation. For the approximation, a Koch curve of level 0 is just a line segment. For N > 0, a Koch curve of level N is made up of 4 smaller-sized level (N-1) curves. To draw it with turtle graphics, you need to be careful about the sizes and the angles between the pieces. (Hint: The angles inside an equilateral triangle are 60 degeres.) This picture shows Koch curves of various recursion levels. The last one is a pretty good approximation of the real Koch curve:

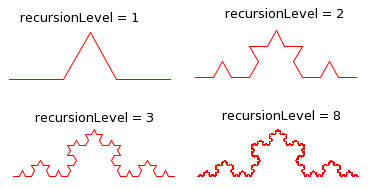
The main program should place the turtle at the desired starting point for the curve and then call your koch() method with a reasonable value for the recursion level. Alternatively, you can do something like what I did with the Sierpinski triangle, where I showed a series of triangles with increasing recursion levels.

For the remaining three turtle graphics exercises, you should choose three of the following recursive drawings, and write recursive methods to draw them:

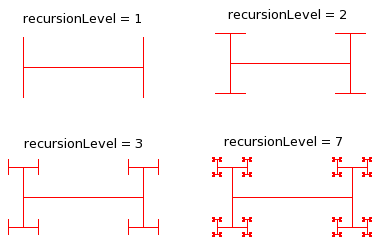Recursive "I-bar." An I-bar of level 0 is just a line segment. An I-bar of level N consists of a line segment with a smaller-sized, rotated I-bar of level (N-1) on each end. (Hint: The turtle should start at the center of the bar and should return to that position after drawing the bar.)

Sierpinski carpet. A Sierpinski carpet of level 0 is just a square. A Sierpinski carpet of level N consists of 8 1/3-sized Sierpinski carpets of level (N-1). The picture shows a level-5 carpet. It takes a long time to draw a carpet with level greater than 5, but there is a bigger picture of a level-6 carpet at this link.

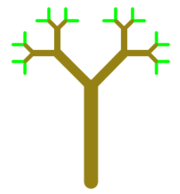
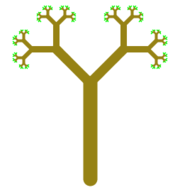Improved tree. This is a version of the tree example that we covered in class, in which I have varied the color and line width while drawing the tree. (Level-0 trees are drawn in green.) A level-4 tree and a level-7 tree are shown.

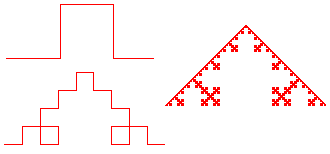Square Koch. This is a version of the Koch curve that uses squares instead of triangles. Square Koch curves of level 1, 2, and 8 are shown.

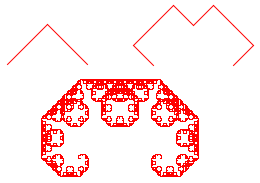C Curve. A rather pretty thing, composed of two copies of itself at a 90 degree angle. A level-0 curve is a line segment. To get a level-N curve, start by turning 45 degrees, draw the two level-(N-1) curves, then turn 45 degrees again so you are facing in the original direction. If size is the size of the level-N curve, the size of each smaller curve is size/Math.sqrt(2). The pictures were drawn by ccurve(8,1), ccurve(8,3), and ccurve(8,12).

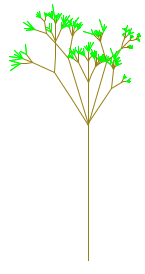
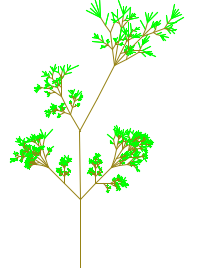Random Factors. It's interesting to add some randomness to recursive drawing. The pictures were drawn by versions of the tree algorithm with some randomness added. You could try to do something similar, or you could think up your own random recursion.

Maze Solver

The final exercise uses the files MazePanel.java and MazeSolver.java. You will only work on MazeSolver.java, which contains the main() routine for the program. If you run MazeSolver without making any changes, it will open a window showing a randomly created maze. (It doesn't do anything else -- you can just close the window.)

The MazePanel class defines the panel that creates and displays the random maze. The maze is made up of a grid of small colored squares. Black squares represent "walls" and white squares represent "corridors." Note that there is a border of black squares all around the edge of the maze. (There is no exit from the maze!)

MazeSolver.java has an instance variable named maze of type MazePanel. This variable has the following methods, which you can use in the program:

• maze.getColor(r,c) -- Returns the color of the square in row r, column c. A null value represents a corridor, which appears as white in the picture.
• maze.setColor(r,c,color) -- Set the color of the square in row r, column c to color. Setting the value to null will make the square white.
• maze.getRows() -- Returns the number of rows in the maze.
• maze.getColumns() -- Returns the number of columns in the maze.

Your job is to add a method to MazeSolver.java that will solve the maze. It is not your job to show the process of solving the maze! The program will solve the maze and display just the final result.

The maze is considered solved if you find a path from location (1,1) to location (maze.getRows()-2,maze.getColumns()-2). These points are the upper left and lower right white squares in the original maze. You should mark the path by setting its color to something other than black or white. You might also want to color squares that your method visits while it is searching for the solution. Here is a picture of a small maze that shows the solution in red; other squares that were visited during the search are colored yellow:

The essential idea of the recursion is: "to solve the maze from (x,y), move one square from that position and try to solve it from there." It's possible that you might try all four directions from (x,y) without finding a solution. One interesting point is how to end the process once you find a solution, since at that point you will be deep in the recursion. One nice way to do it is to return a boolean value from the method. If you find a solution, you can immediately return true; if you try all four directions without finding a solution, you can return false.

Your program can simply call the solver method at the end of the main() routine. (You might need to call maze.repaint() at the end of main().)

If you want to do something fancier, copy the delay() method from TurtleGraphics.java. In the main program, add a delay of a few seconds after the call to window.setVisible. This will give the user a chance to see the unsolved maze. Then call your maze solver method, and call maze.repaint() to put the solved maze on the screen. To get even more fancy, make an infinite loop in which you repeatedly make new random mazes -- by calling maze.create() -- and solve them. The loop will end when the user closes the window.