CS 424: Computer Graphics, Fall 2013
Lab 13: More WebGL
This lab consists of two fairly short WebGL exercises. In the first, you will implement a simple procedural texture in GLSL. In the second, you will use gl.drawElements to draw polyhedral models.
For this lab, you will need all the files from the folder /classes/cs424/lab13-files. You will work on the HTML files Lab13-Ex1.html and Lab13-Ex2.html. The other things in the folder are JavaScript files that are used by the two HTML files and must be present for them to work. You will want to take a look at polyhedra.js, which defines the polyhedral models that you will work with in Exercise 2. You won't need to understand the other three JavaScript files.
You should copy your work for this lab into your homework folder in /classes/cs424/homework by the beginning of the next lab. It should be in a folder named lab13 or something similar.
Exercise 1: A Simple Procedural Shader
A texture varies some property of the surface from point to point, usually based on the texture coordinates that have been assigned to that point. In a procedural texture, the effect of the texture is computed rather than read from an image file. In WebGL, procedural textures can be implemented in GLSL code in the shader program. In this exercise, you will add a simple procedural texture to the program Lab13-Ex1.html. Currently, that program draws models using plain white color. The texture that will apply will make the models look like they are cut out of a 3D checkerboard pattern. The models are relatively large, and the squares of the checkerboard will be one unit big. Here are two examples from my solution to this exercise:
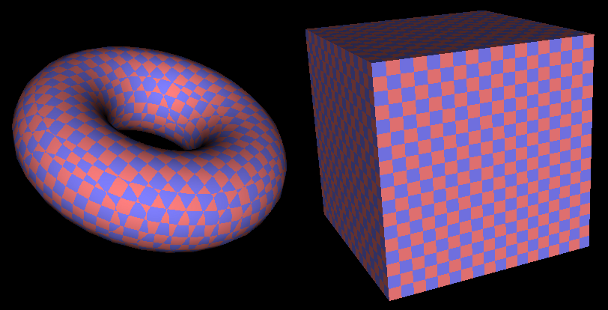
In this example, the checkerboard colors are pink and blue. You can use whatever colors you like.
The checkerboard texture is actually a 3D texture. That is, the color of a point depends on three coordinates, not just two. For the texture coordinates, you should simply use object coordinates, that is, the coordinates that are specified as the values of the coords attribute in the vertex shader. Think of the checkerboard pattern existing in object space, and the model as being cut out of that pattern. The object coordinates of a point on the model tell you where that point is in the pattern.
However, the texture has to be implemented in the fragment shader, not in the vertex shader. This means that you have to get the object coordinates from the variable coords in the vertex shader into a variable in the fragment shader. For that, you need to add a varying variable to the shaders.
Once you have the (x,y,z) object coordinates in the vertex shader, it's pretty easy to implement the checkerboard pattern: Just convert all three coordinates to integers and add them up. If the resulting sum is even, use the first color for the fragment; if it is odd, use the second color.
Now, integers are not really well supported in GLSL. There is no % operator and no bitwise logical operations. However, the operations that you need are available as functions. For a floating point value x, the GLSL function floor(x) rounds x down to the next lowest integer. It gives a floating point result; for example, floor(3.723) is 3.0. And for two floats, the function mod(a,b) computes the remainder when a is divided by b. This means that mod(a,2.0) is 0.0 if a is an even integer and is 1.0 if a is an odd integer. You can use the functions floor and mod to do the math that you need to implement the texture.
Exercise 2: Polyhedron Viewer
For this exercise, you will work with the file Lab13-Ex2.html. Currently, it draws nothing at all. However, it does contain code that allows the user to select models from the polyhedral models defined in the file polyhedra.js. The data for the currently selected model is stored in the global varialbe currentModel. Your job is to make the program draw the model. You can either draw a gray model or, for some extra credit, a randomly colored one. (There is no color data given as part of the model; you have to make it up.) Here are two views of the stellatedDodecahedron model, one in gray and one colored, from my solution to the exercise:

You only need to work in two places in the file, in the function installModel() and in the function draw(). The first of these is called when a model is selected. The second is called to render the scene. You need to add code to installModel() to transfer the data into a format that can be used by WebGL. You need to add code to draw() to render the model. The variable currentModel is already set to refer to the object that contains the model data from polyhedra.js. The format of that data is described in a comment at the top of polyhedra.js, and the socreBall example was handed out in class. The attribute and uniform locations and the buffers that you will need already exist and have been initialized; you just need to use them.
We discussed this example in class. My suggestion is to put all the coordinate data into the aCoordsBuffer VBO. I suggest drawing each face separately, using gl.drawElements and putting the indices for the face into the indexBuffer VBO; it is easiest to redo that in draw() each time you draw a face. Don't forget that the normal vector is a uniform in this program, with a single normal vector being using for an entire face.
If you want to add color, you will have to make up the color data, but note that there is already a color uniform variable that you can use.