A Note About Anaglyph Stereo

To add a little interest to the lab, the program that you will be working on implements an anaglyph stereo view of the objects that you will draw. An anaglyph stereo image is meant to be viewed through red/cyan 3D glasses. (I will give you a pair in lab.) On the screen, the view from the left eye is drawn using only shades of red, and the view from the right eye uses only shades of green and blue. In the program, anaglyph mode is turned on and off by pressing the space bar. Since color anaglyph didn't work very well, the program turns color off when in anaglyph mode. Here's how the program will draw the "cage" that you make at the end of the lab, in anaglyph mode:

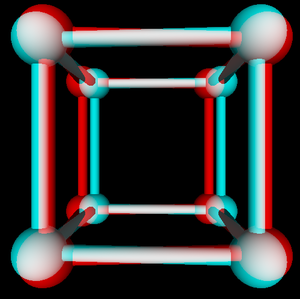
You do not have to do any work for this part of the lab. I will explain how it works in class. However, here's the basic idea:

1. Move the viewer to the position of the left eye, and aim the view towards the object;
2. Draw the scene as usual, but writing only to the red color channel;
3. Clear the depth buffer (but NOT the color buffer!);
4. Move the viewer to the position of the right eye, and aim the view towards the object;
5. Draw the scene as usual, writing only to the green and blue color channel;
6. Go back to drawing to all color channels.

(Do you see why step number 3 is essential?) Note that the transformations have to be applied first, before any modeling transformations.

The only new OpenGL feature that is needed to implement all this is the ability to control which color channels are being written. The function

glColorMask( r, g, b, a );

can do that. It is not mentioned in the textbook. The parameters to glColorMask are boolean values. (For Java, true and false are used; for C, 1 and 0 are used to represent the boolean values.) The parameters r, g, b and a control writing to the red, green, blue, and alpha color channels, respectively. A true value means that it is possible to write to the channel; a false value blocks writing to the channel. In the initial state, of course, all the color channels are enabled. To restore the initial state, call glColorMask with all parameters set to true.

Draw a Shape

For this lab, you will be drawing six objects using OpenGL. When you run the program, hitting one of the number keys 1 through 6 will select the object that is displayed. The program already sets the value of a global variable, objectNumber, to tell you which object to draw. The user can rotate the object using the arrow, PageUp, PageDown, and Home keys. The display() subroutine is called to draw the object. That subroutine in turn calls draw(), and it is inside draw() where you should do your work. (The place is marked with a TODO.)

Object number 1 is a simple 2D shape, which you should draw directly, using glBegin(), glEnd(), glVertex2f(), and glColor3f. You should use different colors for different vertices; just remember that if you use the same vertex twice, you should use the same color in both cases. Here is the shape, with the vertices labeled:

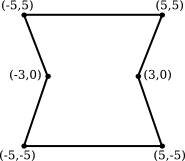
It is possible to make this shape using the primitive GL_TRIANGLE_FAN or GL_QUAD_STRIP. Other primitives are possible, including GL_QUADS and GL_TRIANGLES, but they require a little more work.

Draw a Wireframe Polyhedron

Object number 2 is a wireframe polyhedron. That is, you will just draw the edges of the polyhedron. The particular polyhedron is called a stellated dodecahedron. It has 60 triangular faces. The data for the polyhedron is already in the program, in two two-dimensional arrays named dodecVertices and dodecTriangles.

The first array, dodecVertices, is a 2D array of double that contains the (x,y,z) coordinates of the vertices of the polyhedron. For example, vertex number 13 has coordinates (dodecVertices[13][0], dodecVertices[13][1], dodecVertices[13][1]). You can use these coordinates in the function glVertex3d(x,y,z).

The second array, dodecTriangles, is a 2D array of int. Each row of the array contains three integers, giving the vertex numbers for the vertices of one of the triangular faces of the polyhedron. That is, the integers in dodecTriangles are indices into the vertex array. For example, dodecTriangles[7][0] is the vertex number for the first vertex of face number 7.

Your job is to draw the outline of each of the 60 triangular faces. You can do that by drawing each face as a primitive of type GL_LINE_LOOP. This can easily get confusing. When processing face number i, I suggest that you give names to the vertex numbers for that face. For example,

int v = dodecTriangles[i][j];  // Vertex number for vertex j of face i.

(If you still find this confusing, you can look ahead at the discussion of "Indexed Face Sets" in Subsection 3.4.1. But remember that here you are drawing the edges, not the faces, of the polyhedron.)

Important Note: A wireframe should be drawn with lighting effects turned off! To implement that, you should use the command

glDisable(GL_LIGHTING);  // or gl2.glDisable(GL2.GL_LIGHTING) in Java

before you draw the polyhedron, and

glEnable(GL_LIGHTING);  // or gl2.glEnable(GL2.GL_LIGHTING) in Java

after you draw the polyhedron.

Use GLUT (and Transforms)

Object number 3 is a very simple example of using GLUT and transforms. This is just a warm-up for the remaining objects. The third object is a solid, 3D object that consists of a cone sitting on top of a cylinder:

The cone and the cylinder can be drawn using the GLUT library:

glutSolidCylinder( radius, height, 32, 8 );

glutSolidCone( radius, height, 32, 8 );

(In Java, the method names will be glut.glutSolidCylinder and glut.glutSolidCone.) The first two parameters specify the size of the object. The last two are "slices" and "stacks" and determine how smooth the curved surfaces will be; the values 32 and 8 are fine for this lab.

For this example, use radius = 3 and height = 5.

Both the cone and the cylinder are drawn with the center of their basees at (0,0,0) and with their axes lying along the positive z-axis (that is, pointing directly out of the screen, assuming no transformation has been applied). So, if you just use the above commands, the cone will be inside the cylinder! Obviously, you will need to apply a transformation. The complete object should have its center at (0,0,0) for proper display. It will still be pointing directly at you, so you will have to rotate it to get a better view.

Don't forget to use glPushMatrix() and glPopMatrix() to limit the effect of any transformation that you apply!

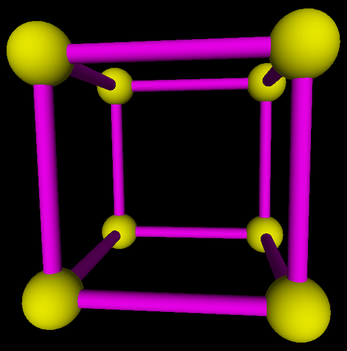
Build a Cage

Objects number 4, 5, and 6 are stages in building a "cage" out of cylinders and spheres. The cage, object number 6, has eight spheres at the vertices of a cube. The centers are the points (-4,-4,-4), (-4,-4,4), (-4,4,-4), etc. There is a narrow cylinder lying along each edge of the cube. You should use different colors for the cylinders and for the spheres. Note that a sphere can be drawn using the GLUT function

glutSolidSphere( radius, 32, 32 );

or glut.glutSolidShpere for Java. The center of the sphere is at (0,0,0). The first parameter is the radius. The other two parameters are, again, "slices" and "stacks"; you can use the value 32 for this lab.

Object number 4 is a "bar" consisting of a cylinder with a sphere at each end. The cylinder lies along the x-axis, and the centers of the spheres are at (-4,0,0) and (4,0,0):

You should write a subroutine to draw the bar. Note that for Java, you will need to pass gl2 as a parameter to the subroutine.

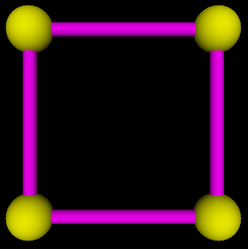
Object number 5 is square shape that can be made out of two copies of the bar, plus two additional cylinders. The square lies in the xy-plane, and the centers of the four spheres are at (-4,4,0), (4,4,0), (-4,-4,0), and (4,-4,0). Again, you should write a subroutine to draw this:

Finally, object number 6 is the full cage, which can be made from two copies of the square, plus four additional cylinders: