CS424 Notes, 15 February 2012

• The Depth Buffer and the Depth Test
  • When making 2D images of 3D scenes, perhaps the very first issue that comes up is the hidden surface problem: how to make sure that when one object is in front of another from the perspective of the viewer, the one that is shown in the image is the one that is in front. If you just naively draw the objects in some random order, it's quite possible that the back object will be drawn before the front object. How do we make sure that it's still the front object that is shown?
  • The simplest idea would be to always draw primitives in back-to-front order, from the perspective of the viewer. This is called the painter's algorithm. One problem with this is that the back-to-front ordering depends on where the viewer is located, so if you change the view, you have to re-sort the primitives into the new back-to-front order. Even then, you still have the problem of self-intersecting primitives, where one primitive is in front of another at some points but in back of it at other points. (And you can get ordering problems even without self-intersection.)
  • Another approach -- the one used in OpenGL -- is to use a depth buffer. A depth buffer contains one number for each pixel in the image. That number represents the z-coordinate (in the clip coordinate system) of the point that is currently visible in that pixel. Recall that in the clip coordinate system, the z-coordinate has a restricted range and increases in the direction that points out of the screen. (Note: The depth buffer is sometimes referred to as a z-buffer.)
  • Before drawing anything, the depth buffer has to be initialized so that every pixel has the maximum z-value, meaning that the background color is currently visible at that point.
  • When a new fragment (fresh from the fragment shader) is applied to the pixel, the depth test is applied: The z-coordinate of the new fragment is compared with the z-coordinate in the depth buffer. If the new fragment has a smaller z-coordinate, the the new fragment lies in front of the object that is currently displayed in the pixel, in that case, the fragment color replaces the current color of the pixel, and the fragment z-coordinate replaces the current value in the depth buffer. If the new fragment has a greater or equal z-coordinate than the value in the depth buffer, the fragment is discarded and the pixel color and the depth buffer value remain unchanged. (Note: The pixel color is stored in what is called the color buffer.)
  • Because of the inexactness of floating point calculations, there can be a problem when the z-coordinates of two surfaces are mathematically equal. The computed z-coordinates might not be exactly equal, and in fact the one that is greater might vary from point to point. If the depth test is applied to the objects, one object will be visible at some points while the other object is visible at other points. Here is an example:

    

    ON the left, three squares of different sizes and colors were drawn. The squares should have the same z-coordinates. You might expect that the one that is drawn last will be the one that is visible, but in fact the one that comes out on top varies seemingly at random from point to point. The image on the right would be produced if the depth test is disabled. It could also be produced with the depth test enabled, by adjusting the z-coordinates of the objects slightly.
  • The depth test is disabled by default in OpenGL. We have not been using it for 2D graphics. For 3D graphics, you have to enable it by calling

        gl.enable(gl.DEPTH_TEST);

    Usually, this can be done once, in the init method. To turn the depth test off, use gl.disable(gl.DEPTH_TEST).
  • You also have to make sure that the depth buffer gets cleared before you start drawing a scene. (Strange things can happen if you forget to do this!). You can clear the depth buffer by calling gl.clear(gl.DEPTH_BUFFER_BIT). It is more common to clear the depth buffer and the color buffer at the same time by calling

        gl.clear( gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT );

    (Now we see why gl.clear() has a parameter: In this case, gl.COLOR_BUFFER_BIT and gl.DEPTH_BUFFER_BIT are ORed together to tell gl.clear() to clear both buffers.)
  • You might have noticed that my discussion of the depth buffer assumes that the objects in the scene are opaque. Transparent objects are a problem for the depth buffer algorithm -- and because of this, OpenGL does not automatically handle transparency. In order for alpha blending to handle transparency correctly, translucent objects should really be drawn in back-to-front order, with all the difficulties that that implies. The usual advice for doing transparency in OpenGL is to draw all the opaque objects with the depth test enabled. The turn off writing to the depth buffer, and draw the translucent objects in back-to-front order. [It is possible to turn off writing to the depth buffer, but still do the depth test, by calling gl.depthMask(false).] This ensures that translucent objects that are behind opaque objects are hidden. Unfortunately, this leaves us with all the difficulties of back-to-front ordering, which is difficult to do in a general way.
• Normal Vectors and Lighting
  • As we move into 3D, we need to take account of the effects of lighting on a scene. Lighting is a major visual cue for three-dimensional vision. Without lighting, objects appear flat. Lighting makes them look three-dimensional.
  • An object in the real world is visible because of the light that reflects from it (or that passes through it, if it is transparent). In the simplified model that is used for basic computer graphics, there are two types of reflection, specular reflection and diffuse reflection. In specular, or mirror-like, reflection, light rays bounce off a surface at the same angle at which they hit the surface. In diffuse reflection, light bounces off the surface in all directions. A shiny red car has a lot of specular reflection; a dull red brink has mostly diffuse reflection.

    

  • For specular reflection, what the viewer sees depends strongly on the angle at which the light hits the surface. Diffuse reflection is visible at all angles, but what the user sees still depends on the angle. This is because the amount of light reflected per unit area depends on the angle at which the light strikes the surface.

    

    For diffuse reflection, an area that is directly illuminated by a light will look brighter than an area that the light strikes at a shallow angle.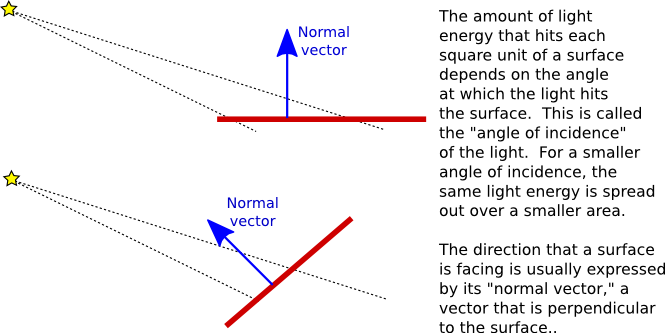
  • The normal vector to a surface at a point on the surface is a vector that points in the direction that the surface is facing. For a curved surface, the direction varies from point to point on the surface. For a flat surface, the direction at each point is the same.
  • A vector has a length and a direction. For normal vectors, we are really only interested in the direction, so usually unit normal vectors are used. A unit normal is a normal vector of length one. Unit normals are very important for lighting calculations.
  • A vector in three dimensions is given by an ordered triple of numbers. The three numbers give the change in x, the change in y, and the change in z from the base of the vector to its head. So, when we specify a normal vector for computer graphics, it looks the same as a point: It's simply three floating point numbers.
• Normal Vectors in OpenGL
  • In OpenGL-style graphics, you can specify a normal vector for each vertex of a primitive, giving the direction of the surface at that vertex. (This is in addition to the vertex coordinates and possibly texture coordinates for the vertex.)
  • In the old-fashioned OpenGL fixed-function pipeline, the normal vector and information about lighting were used to compute a color for each vertex of a primitive. Then that color was interpolated to the interior of the primitive. However, this gives only a rough approximation of the correct lighting for interior points. (This this type of lighting is called Gouraud shading.) A better approximation can be obtained by interpolating the normal vectors from the vertices to the interior points and then doing the lighting calculation at each point of the primitive. (This type of lighting is called Phong shading.) Phong shading was never an option is the fixed-function pipeline. With the programmable pipeline, it's easy to do. It does require more calculation, but I've read that even real-time computer games use it, for its increased realism.
  • When using normal vectors in WebGL, you will need another vertex attribute to specify the normal vectors for the vertices, and you will need an array buffer to hold the normal vectors.
  • Of course, there is no need for normal vectors unless you also have "lights" in your scene. We will return to lighting in much more detail later. For our first examples, we will use a simple lighting model in which white light shines on the scene from the direction of the viewer, and we will only use diffuse reflection.
• Normal Vectors for Surfaces
  • Suppose that V is a vertex of a primitive triangle T. What normal vector should we use at V? At first, it might seem like we should use a vector perpendicular to T. However, if we are using T to approximate a curved surface, that's not true! What we want is a vector that is perpendicular to the surface that is being approximated. To calculate the way that the light would interact with the surface, we need a vector that is perpendicular to the surface that is being approximated, not to the triangle.
  • This is particularly important for vertices that are shared by two or more primitives. In this illustration, the thick blue lines represent primitive (viewed edge-on):

    

    For the top image, we imagine that the primitives are approximating a curved surface, and normal vectors perpendicular to the primitive are used. When a vertex is shared by two primitives, then the vertex is actually used twice, once while drawing each primitive. It's important that the same normal vector be used for the vertex in both primitives; this makes the shading on the two primitives fit together nicely. In the second version, normal vectors perpendicular to the primitives are used. For a vertex that is shared by two primitives, a different normal vector is used when each primitive is drawn. This gives a "faceted" appearance when the surface is rendered, which would be appropriate if the surface itself is literally faceted rather than smooth. Here are two surfaces drawn using the two ways of assigning normal vectors to vertices: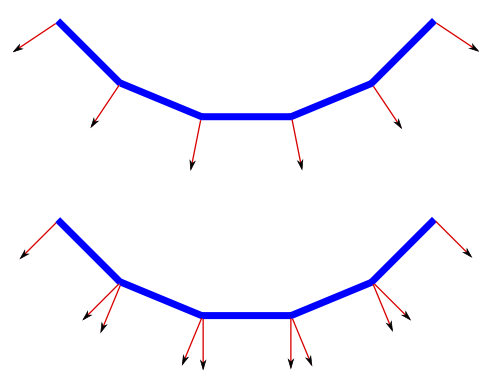

    

    Note that only the normal vectors differ between the two surfaces. The geometry is identical, and if you look at the boundary of the top surface, you will see that it is still made up of geometrically flat pieces.
  • So, where do normal vectors come from, if they are not simply perpendiculars to the primitive triangles? If you have equations for the surface, such as sphere or cylinder, you can compute the normals mathematically. If all you have are the primitives, you can still make the surface look curved by using the same normal vector for the vertex in all the primitives that share it. A common approach is to take the average of the perpendicular vectors to all the primitives that share the vertex.
  • You have seen "smooth" versus "flat" renderings of meshes in Blender. In flat shading, normal vectors perpendicular to the primitives are used. In smooth shading, normals are probably computed using the averaging technique. Note that making a mesh smooth does not change the geometry of the mesh; it only changes the normal vectors that are used in lighting calculations.
  • "Bump mapping" is a technique in which the value of a texture is used to vary the normal vector from point to point on a surface, giving the surface a bumpy appearance in a pattern that reflects the texture. Again, bump mapping does not change the actual geometry, only the lighting calculations. (Another technique, called displacement mapping, does change the geometry by actually moving the vertices -- look for bump mapping and displacement mapping in the lab tomorrow!)