CS424 Notes, January 30

CS424 Notes, 30 January 2012

First, a left-over item from last Wednesday...
- When drawing a primitive, attribute values for the vertices of the primitive are ordinarily read from an array. However, it is possible that you might want to use the same attribute value for the all the vertices of the primitive. There are actually two ways to provide attribute values: in an array, or as a single value for all vertices. You tell the GL which one to use by calling gl.enableVertexAttribArray(attribLocation) or gl.disableVertexAttribArray(attribLocation), where attribLocation is the location of the attribute in the current shader program, as returned by gl.getAttribLocation. Note that the default state is for the vertex attribute array to be disabled, so you have to enable it if you want to use an array (which is the most usual case).
- For example, suppose that there is a vertex attribute of type vec4 whose location is colorLoc. To use the same color value -- say, red -- as the attribute at each vertex, you could say (before calling gl.drawArrays):
```
   gl.disableVertexAttribArray(colorLoc);
   gl.vertexAttrib4f(colorLoc, 1, 0, 0, 1);
```
- To use a different color for each vertex, you would store the colors in an array -- say, colorArray -- and you would need an array buffer to hold the color data on the GPU. Assuming that that buffer is colorBuffer, you could say (before calling gl.drawArrays):
```
   gl.enableVertexAttribArray(colorLoc);
   gl.bindBuffer(gl.ARRAY_BUFFER, colorBuffer);
   gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(colorArray), gl.STATIC_DRAW);
   gl.vertexAttribPointer(colorLoc, 4, gl.FLOAT, false, 0, 0);
```

Geometric Transforms

A coordinate transformation modifies the coordinates of all the points in an object. In computer graphics, we mostly use affine transformations. A two-dimensional affine transformation modifies the (x,y) coordinates of a point from (x_old,y_old) to (x_new,y_new) where
```
   x_new  =  a * x_old  +  c * y_old  +  e
   y_new  =  b * x_old  +  d * y_old  +  f
```
for some constants a, b, c, d, e, and f.
If you apply an affine transform to a pair of parallel lines, the result will be another pair of lines that are also parallel. This is defining property of "affine" transformations.
An affine transform in 2D can be represented by a 3-by-3 matrix
To apply the transformation to a point (x,y), multiply the vector (x,y,1) by the matrix, and then discard the 3rd coordinate:

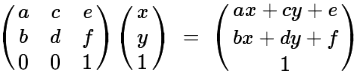
Affine transforms can express a variety of "geometric transformations." The basic geometric transformations are translation, rotation, and scaling:

	Translation moves each point horizontally and/or vertically by a set amount. This can be expressed as an affine transformation with equations x_new = x_old + e y_new = y_old + f In the picture, each point moves 5 units horizontally and 2 units vertically.
	Rotation about the origin rotates each point through a given angle, θ, about the origin, (0,0). As an affine transformation, x_new = c * x_old - s * y_old y_new = s * x_old + c * y_old where c = cos(θ) and s = sin(θ). In the picture, θ is -135 degrees.
	Scaling about the origin multiplies the x coordinate by a certain amout, sx, and the y coordinate by a certain amount, sy. As an affine transformation, x_new = sx * x_old y_new = sy * y_old If sx = sy, you have uniform scaling, which is the most common case. In the picture, sx is 3 and sy is 2.

It is possible to "compose" transformations, that is, to follow one transformation by a second transformation. When you compose affine transformations, the result is another affine transformation. Furthermore, when you compose two transformations, the matrix for the resulting transformation is obtained by matrix multiplication of the matrices for the two transformations. This is really the main point of using matrices.
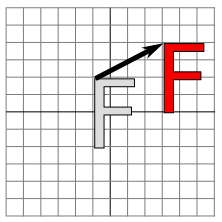
Matrix multiplication -- and so composition of affine transformations -- is non-commutative. That is, the result depends on the order in which you do things. The picture on the left below shows what happens if you first rotate the "F" by 90 degrees then translate it by (4,0). The picture on the right shows what happens if you do the same transformations in the opposite order, first translate by (4,0), then rotate by 90 degrees:

Any affine transformation can be create as a composition of a sequence of translations, rotations, and scalings, but it's not necessarily easy to see how to do so. For example, consider "shear":

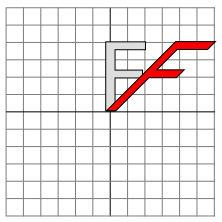
Shearing in the x-direction leaves the x-axis fixed but moves other points horizontally by an amount proportional to the distance from the x-axis. This has the affine transformation

       x_new  =  x_{old  +  s * y_old
       y_new  =  y_old}

In the picture, s = 1.

In particular, rotation through the angle θ about the point (a,b) can be achieved by the sequence of transformations

   1. translate by (-a,-b)   [ moves (a,b) to (0,0)  ]
   2. rotate by θ            [ about the point (0,0) ]
   3. translate by (a,b)     [ moves (0,0) to (a,b)  ]

The class AffineTransform2D
- The JavaScript file affinetransform2d.js implements support for affine transformations in two dimensions. This file defines the class AffineTransform2D, and an object of this class represents an affine transformation.
- The constructor new AffineTransform2D() creates a transform that is initialized to the identity transformation, which represents the "transformation" that does not make any change at all. If transform is of type AffineTransform2D, then the following methods are available for combining transform with another affine transformation:
  - transform.translate(dx,dy) --- multiply transform on the right by a translation by the amount (dx,dy)
  - transform.rotate(theta) --- multiply transform on the right by a rotation about the origin through the angle theta
  - transform.rotateAbout(x,y,theta) --- multiply transform on the right by a rotation about the point (x,y)
  - transform.scale(s) --- multiply transform on the right by a uniform scaling by a factor of s (about the origin)
  - transform.scale(sx,sy) --- multiply transform on the right by a scaling of sx horizontally and sy vertically
  - transform.scaleAbout(x,y,s) --- multiply transform on the right by a uniform scaling by a factor of s about the point (x,y)
  - transform.scaleAbout(x,y,sx,sy) --- multiply transform on the right by a scaling of sx horizontally and sy vertically about the point (x,y)
  - transform.xshear(s) --- multiply transform on the right by a shear of s in the x direction
  - transform.times(t) --- multiply transform on the right by another AffineTransform2D t
- Note that these methods actually modify transform. Each of these methods also returns the modified transform as its return value. This makes it possible to "chain" transformations. For example: transform.rotate(90).translate(4,0). This has the same effect as saying transform.rotate(90) followed by transform.translate(4,0).
- Important point: transform.rotate(90).translate(4,0) represents the transformation that first translates a point by (4,0) and then rotates it by 90 degrees! That is, the order in which transformations are applied to a vector is the opposite of the order in which they are composed. (This is because when you do the matrix multiplication, the operation that is applied first to the vector is the matrix that is closet to the vector. This is the one that is furthest to the right, that is, the last one that was composed into the transformation.)
Modeling Transformations in WebGL
- In computer graphics an object is ordinarily specified in the coordinate system that is most appropriate for the object. These coordinates are called object coordinates. In general, in object coordinates (0,0) is at the center of the object (or at least at a convenience reference point), and the unit of size is chosen to be some convenient value for the object that is being modeled.
- The coordinates on the scene as a whole are called world coordinates. The object is placed into the scene by applying a transformation. This transformation is called the modeling transformation. It transforms object coordinates to world coordinates. (A different modeling transformation can be used for each object in the scene.)
- Modeling transformations are pretty much always affine transformations. The modeling transform in WebGL can be applied in the vertex shader, using a uniform matrix variable. For 2D graphics, the matrix can be a 3-by-3 matrix of type mat3.
- Suppose transform is an AffineTransform2D in the JavaScript program representing the modeling transformation, and transformLoc is the location of the mat3 uniform that represents the modeling transform in the vertex shader, then the value of the mat3 can be set by saying
```
   gl.uniformMatrix3fv( transformLoc, false, transform.getMat3() );
```
  where transform.getMat3() is a method that returns the 3-by-3 matrix representing the transformation, as an array of numbers in the column-major order required by WebGL. (The second parameter to gl.uniformMatrix* has to be false; this is a vestige of desktop OpenGL.)
- About order of operations... Consider
```
   transform.rotate(90);
   transform.translate(4,0);
   gl.uniformMatrix3fv( transformLoc, false, transform.getMat3() );
   // now draw an object
```
  The translation applies to the thing that comes after it, that is, to the object. The rotation also applies to the thing that comes after it, that is, to an object that has already been translated. The translation is applied to the object first, then the rotation is applied to the result. So, it makes sense that modeling transformations are applied to objects in the opposite order to the order in which they appear in the code.
World-to-clip transformation
- The world coordinates used in a scene still have to be transformed into WebGL's default coordinate system, which is referred to as clip coordinates. In 3D, this transformation is called projection -- or maybe a combination of projection and "viewing". For 2D graphics, I will just refer to it as the world-to-clip coordinate transformation.
- The world-to-clip coordinate transformation can be represented as another affine transform or, in the vertex shader, as a uniform variable of type mat3. The world-to-clip transform is applied to the result of the modeling transform to give the clip coordinates that will be passed on to the fragment shader.
- In the examples for the second part of Lab 3, the modeling transform and the coordinate transform are represented by separate mat3 variables in the fragment shader. The coordinates of the vertex are represented by a vec2. To apply the transformations, a 1.0 is added to the vec2, giving a vec3, and the resulting vector is multiplied by the transformation matrices. Here is the complete source code for the vertex shader:
```
   attribute vec2 vertexCoords;
   uniform mat3 transform;         // The modeling transformation.
   uniform mat3 coordTransform;    // the world-to-clip transformation.
   void main() {
      vec3 pt = coordTransform * transform * vec3(vertexCoords, 1.0);
      gl_Position = vec4( pt.x, pt.y, 0.0, 1.0 );
   }
```
  In the last statement, we need a vec4 to represent the clip coordinates. The x and y coordinates come from the transformed point. The z and w coordinates are 0 and 1, which are the appropriate values for 2D graphics.