CS424 Notes, 5 March 2012

• Some functions from gl-matrix.js
  • mat4 functions that return a 4-by-4 matrix (and have an optional "destination" parameter):
    • mat4.identity(), (returns a matrix representing the identity transform, which represents no change at all)
    • mat4.create(mat), for a 4-by-4 matrix mat (creates a new matrix that is a copy of mat)
    • mat4.translate(mat, vec), for a 4-by-4 matrix mat and a 3-vector vec
    • mat4.scale(mat, vec), for a 4-by-4 matrix mat and a 3-vector vec
    • mat4.translate(mat, vec), for a 4-by-4 matrix mat and a 3-vector vec
    • mat4.rotate(mat, radians, axis), for a 4-by-4 matrix mat and a 3-vector axis
    • mat4.rotateX(mat, radians), rotation about the x-axis
    • mat4.rotateY(mat, radians), rotation about the y-axis
    • mat4.rotateZ(mat, radians), rotation about the z-axis
    • mat4.inverse(mat), for a 4-by-4 matrix mat (returns the inverse matrix, that "undoes" mat); returns null if no inverse exists
  • More mat4 functions, which create commonly used mat4 viewing and projection matrices [see below].
    • mat4.lookAt(eye,center,up), where eye, center, and up are 3-vectors (creates a viewing transform matrix the puts the camera/viewer at eye, looking in the direction of center, and oriented so that up appears to point upwards in the view)
    • mat4.ortho(left,right,bottom,top,near,far), where the parameters are numbers (creates an orthogonal projection matrix)
    • mat4.frustum(left,right,bottom,top,near,far), where the parameters are numbers (creates a perspective projection matrix)
    • mat4.perspective(fovy, aspect, near, far), where the parameters are numbers (creates a perspective projection matrix in a more convenient way)
  • Note: gl.lookAt is covered in last Friday's notes. We will look at the general idea of projection today, and we'll get to the gl-matrix.js projection functions on Wednesday.
• Modeling and Viewing Example
  • When setting up the view with gl.lookAt, the gl.lookAt is the first function called. It creates a transform matrix that represents the viewing transformation, with no modeling transform. Any modeling transforms are then applied to the viewing transform matrix, before objects are drawn. Remember that the objects will then be first transformed by the modeling transform, to place then in the world. The the viewing transform is applied to show the world from the point of view of the camera/viewer.
  • Here is an example that uses some very simple hierarchical graphics:

        /**
         * Draws one frame; time is the time in milliseconds since the animation
         * started.  The picture shows two rotating cubes on the ends of a
         * rotating rod (which is itself just a scaled cube).  Note that the
         * function, cube(), draws a cube including applying the modelview matrix;
         * popMatrix() and pushMatrix() save and restore the modelview transform.
         */
        function draw(time) {
            gl.clearColor(0,0,0,1);
            gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
            gl.uniformMatrix4fv(projectionUniformLocation, false, projection );
            modelview = mat4.lookAt( [5,5,10], [0,0,0], [0,1,0] );
            if (time > 5000) {  // (start this rotation after 5 seconds)
               mat4.rotateY(modelview, ((time-5000)/1000)*(Math.PI/3) );
            }
            pushMatrix();
            mat4.translate(modelview, [-1.5,0,0] );
            mat4.rotateX(modelview, (time/1000)*(Math.PI/1.13) );
            mat4.scale(modelview, [0.5,0.5,0.5]);
            cube();
            popMatrix();
            pushMatrix();
            mat4.translate(modelview, [1.5,0,0] );
            mat4.rotateX(modelview, -(time/1000)*(Math.PI/.873) );
            mat4.rotateY(modelview, Math.PI);
            mat4.scale(modelview, [0.5,0.5,0.5]);
            cube();
            popMatrix();
            mat4.scale(modelview, [1.1, 0.1, 0.1]);
            cube();
        }
        

    The picture produced by this draw function looks like this:

    

    The live program is at http://math.hws.edu/eck/cs424/s12/notes/mar5/gl-matrix-cube.html.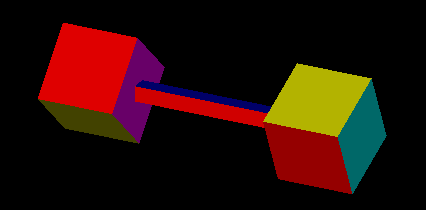
• Projection.
  • Note: WebGL, like OpenGL ES 2.0, does not actually have any notion of projection! You are responsible for setting up and applying a projection transformation. OpenGL with the fixed-function pipeline, on the other hand, had several standard ways to set up projection transformations. The gl-matrix.js library includes some functions that create projection matrixes in the same standard way that traditional OpenGL programmers are used to, and that's what I will discuss here
  • "Projection" usually refers to projecting a 3-dimensional scene down to a 2-dimensional image (although that's not quite what it means in OpenGL).
  • There are two basic types of projection: orthogonal and perspective.
  • Perspective projection gives a realistic view. That is, it shows what you would see if the OpenGL display rectangle on your computer screen were a window into an actual 3D world (one that could extend in front of the screen as well as behind it). It shows a view that you could get by taking a picture of a 3D world with a camera. In a perspective view, the apparent size of an object depends on how far it is away from the viewer. Only things that are in front of the viewer can be seen. In fact, the part of the world that should in view is an infinite pyramid, with the viewer at the apex of the pyramid.
  • However, OpenGL can't actually show everything in this pyramid, because of its use of the depth buffer to solve the hidden surface problem. Since the depth buffer can only store a finite range of depth values, it can't represent the entire range of depth values for the infinite pyramid that is theoretically in view. Only objects in a certain range of distances from the viewer are shown in the image that OpenGL produces. That range of distances is specified by two values, near and far. Both of these values must be positive numbers, and far must be greater than near. Anything that is closer to the viewer than the near distance or farther away than the far distance is discarded and does not appear in the rendered image. The volume of space that is represented in the image is thus a "truncated pyramid." This pyramid is the view volume:

    

    The view volume is bounded by six planes -- the sides, top, and bottom of the pyramid. These planes are called clipping planes because anything that lies on the wrong side of each plane is clipped away.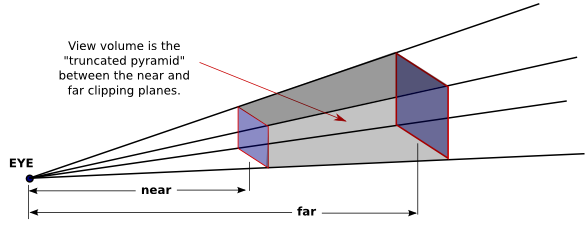
  • Orthographic projections are comparatively easy to understand: A 3D world is projected onto a 2D image by discarding the z-coordinate of the eye-coordinate system. This type of projection is unrealistic in that it is not what a viewer would see. For example, the apparent size of an object does not depend on its distance from the viewer. Objects in back of the viewer as well as in front of the viewer are visible in the image. Orthographic projections are still useful, however, especially in interactive modeling programs where it is useful to see true sizes and angles, unmodified by perspective.
  • In fact, it's not really clear what it means to say that there is a viewer in the case of orthographic projection. Nevertheless, in OpenGL there is a viewer, which is located at the eye-coordinate origin, facing in the direction of the negative z-axis. Theoretically, a rectangular corridor extending infinitely in both directions, in front of the viewer and in back, would be in view. However, as with perspective projection, only a finite segment of this infinite corridor can actually be shown in an OpenGL image. This finite view volume is a parallelepiped -- a rectangular solid -- that is cut out of the infinite corridor by a near clipping plane and a far clipping plane. The value of far must be greater than near, but for an orthographic projection, the value of near is allowed to be negative, putting the "near" clipping plane behind the viewer, as it is in this illustration:

    

    Note that a negative value for near puts the near clipping plane on the positive z-axis, which is behind the viewer.