CS424 Notes, 16 March 2012

• Lights in OpenGL
  • Standard OpenGL has several types of "light": directional, positional, and spotlight. It can support at least eight lights in a scene. Each light can be enabled or disabled; a light contributes illumination to a scene only if it is enabled. In addition, there is a global ambient light intensity -- a vec4 representing the level of global ambient illumination.
  • A light has a position. The position is a vec4, (x,y,z,w), which is interpreted in homogeneous coordinates. The w coordinate is usually 0 or 1. If w is 0, then the position of the light is considered to be at a point at infinity in the direction of the vector (x,y,z). This gives a directional light, or sun, in which all the light rays are parallel, pointing in the direction of the arrow from (x,y,z) to (0,0,0). If w is 1, then the light source is a positional light, or point source, located at (x,y,z), in which the light rays radiate out from the point (x,y,z). (If w is not equal to 1 or 0, then the light is a positional light at (x/w,y/w,z/w).) A spotlight is a positional light that only emits a cone of light in some direction. The direction and angle of the light cone are settable properties of the light.
  • A light source has a diffuse intensity, a specular intensity, and an ambient intensity. These are vec4's that you can think of as the color of the light, although they are not colors in the same sense as material colors, and the red, green, and blue components can be greater than one. The diffuse and specular intensities determine how the light interacts with diffuse and specular material colors. The ambient intensity is a little different: When the light is enabled, its ambient intensity is added to the global ambient intensity, increasing the amount of ambient light in the environment. (Diffuse and specular intensities are usually the same. The ambient light is most often black, that is, zero.)
  • When you have a point source of light, the amount of illumination that a suface gets from the light depends on the distance of the surface from the light. This is called "attenuation" of the light. Physically, the equation for attenuation should be \[ surface\_illumination = \frac{light\_intensity}{r^2} \] where r is the distance from the surface to the light. However, this equation apparently doesn't really work well visually in computer graphics. So, in OpenGL, you can set up an attenuation function for a light source of the form \[ surface\_illumination = \frac{light\_intensity}{a+br+cr^2} \] where a, b, and c are any constants. You might even use b = c = 0 and a = 1, which gives no attenuation at all -- and in fact, that's the default!
• Some Linear Algebra
  • In the OpenGL lighting model, the interaction of light with materials produces the visible color of a point on a surface. The interaction is given by a mathematical formula known as the lighting equation. In order to understand it, you need to know something about certain linear algebra operations and their physical meaning.
  • A 3D vector (or vec3) is a triple of three numbers \( (x,y,z) \). A vector has a length, which is given by \( \sqrt{x^2+y^2+z^2} \). If the length is non-zero, then the vector also has a direction -- the direction of the arrow from the point \( (0,0,0) \) to the point \( (x,y,z) \).
  • A vector is often represented by an arrow, but the vector does not have a position. If you draw two arrows at different places, and if the two arrows have the same length and the same direction, then they are the same vector.
  • If \( P_1 = (a_1,b_1,c_1) \) and \( P_2 = (a_2,b_2,c_2) \) are points, then Then we can visualize an arrow that starts at \(P_1\) and ends at \(P_2\). That arrow represents a vector, which is given by \( (a_2-a_1,b_2-b_1,c_2-c_1) \).
  • A unit vector is a vector with length 1. If \(v=(x,y,z)\) is any non-zero vector and the length of \(v\) is \(d\), then the vector \((x/d,y/d,z/d)\) is a unit vector that points in the same direction as \(v\). To normalize a vector means to divide the vector by its length to get a unit vector in the same direction. (The term "normalize" here has nothing to do with "normal vectors", unfortunately).
  • If \( v_1=(x_1,y_1,z_1) \) and \(v_2=(x_2,y_2,z_2) \) are vectors, their dot product is defined as \( v_1\cdot v_2=x_1y_1+x_2y_2+x_3y_3 \). The dot product is also called the inner product.
  • The dot product has geometric meaning: If \( v_1 \) and \( v_2 \) are unit vectors (that is, with length 1), then their dot product satisfies \( v_1 \cdot v_2 = \cos(\theta) \), where \(\theta\) is the angle between \( v_1 \) and \( v_2 \). If \( v_1 \) and \( v_2 \) are any vectors, \( v_1\cdot v_2 = 0 \) if and only if \(v_1\) is perpendicular to \(v_2\).
  • \( v_1\cdot v_2 > 0 \) if the angle between \( v_1 \) and \( v_2 \) is less than ninety degrees; \( v_1\cdot v_2 < 0 \) if the angle between \( v_1 \) and \( v_2 \) is greater than ninety degrees. This will be useful in determining whether a surface is pointed towards a light source or away from it.
  • Although it doesn't have immediate relevance to lighting, there is another type of product for 3D vectors. If \( v_1=(x_1,y_1,z_1) \) and \(v_2=(x_2,y_2,z_2) \) are vectors, their cross product is another vector, denoted \( v_1\times v_2 \). The formula for this product is not really important, but the geometric meaning is: First, \(v_2=(x_2,y_2,z_2) \) is zero if and only if \(v_1\) and \(v_2\) are parallel, that is if they point in the same direction or in opposite directions. More important, if \(v_1\) and \(v_2\) are not parallel, then \( v_1\times v_2 \) is a vector that is perpendicular to both \(v_1\) and \(v_2\). You can use this fact to find a normal vector to a polygonal face of a solid. (Note: the direction of \( v_1\times v_2 \) is determined by the right-hand rule.)
  • The WebGL Shading language has standard functions for working with vectors. So does gl-matrix.js, for use in JavaScript.
    
    

    	GLSE	gl-matrix.js
    Vector represented by	An array	The type vec3
    Vector from point p1 t0 p2	vec3.subtract(p2,p1)	p2 - p1
    Length of a vector v	vec3.length(v)	length(v)
    Normalizing a vector v	vec3.normalize(v) (modifies v)	normalize(v) (returns the normalized vec3)
    Dot product of v and w	vec3.dot(v,w)	dot(v,w)
    Cross product product of v and w	vec3.cross(v,w)	cross(v,w)

• The Lighting Equation
  • The goal of "lighting" is to produce a color, (r,g,b,a), for a point on a surface. The alpha component, a, is easy -- it's simply the alpha component of the diffuse material color at that vertex. But the calculations of r, g, and b are fairly complex.The lighting equation is the mathematical formula that determines the color of a point on a surface based on the material properties of the surface and the lights in the scene. It takes into account the ambient light as well as the contribution from each light source that shines on the surface. The contribution from a given light source can be computed in terms of several unit vectors: A unit normal vector \(N\) to the surface, which points in the direction that the surface is facing; the unit normal \(L\) that points from the surface in the direction of the light source (which can be either positional or directional); the reflection direction \(R\), such that the angle between \(R\) and \(N\) is equal to the angle between \(R\) and \(L\); and a unit vector \(V\) that points in the direction from the surface to the viewer. The vectors are illustrated in this picture:

    

    Note that if the angle between \(N\) and \(L\) is greater than 90 degrees, then the light is actually behind the surface and does not contribute the illumination of the surface at that point. This can be tested by checking whether \(N\cdot L < 0\), where \(N\cdot L < 0\) is the dot product.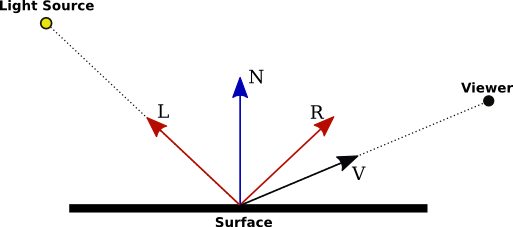
  • When doing the lighting computation, identical computations are done separately for the red, green, and blue color components. Ignoring alpha components, let's assume that the ambient, diffuse, specular, and emissive colors of the material have RGB components \( (ma_r,ma_g,ma_b) \), \( (md_r,md_g,md_b) \), \( (ms_r,ms_g,ms_b) \), and \( (me_r,me_g,me_b) \), respectively. Suppose that the global ambient light intensity is \( (ga_r,ga_g,ga_b) \). Then the red component of the vertex color will be \[ r = me_r + ga_r*ma_r + I_{1r} + I_{2r} + \cdots \] where \( I_{1r} \) is the contribution to the color that comes from the first light source, \( I_{2r} \) is the contribution to the color that comes from the second light source, and so on. A similar equation is used for the green and blue components of the color. This equation says that the emission color is simply added to any other contributions to the color. The contribution of global ambient light is obtained by multiplying the global ambient intensity by the material ambient color, which is just the mathematical way of saying that the material ambient color is the proportion of the ambient light that is reflected by the surface.
  • Next, we need the contribution from each light source. Let \(I\) be one of the light sources in the scene. Let's say that the light has ambient, diffuse, and specular color components \( (la_r,la_g,la_b) \), \( (ld_r,ld_g,ld_b) \), \( (ls_r,ls_g,ls_b) \). Also, let \(mh\) be the value of the shininess property of the material. Then the contribution of light source \(I\) to the red component of the vertex color can be computed as \[ I_r = la_r*ma_r + f*att*spot*\hskip 1.7 in \]\[ \hskip 1.2 in \big( ld_r*md_r*(L\cdot N)+ ls_r*ms_r*max(0,V\cdot R)^{mh} \big) \] with similar equations for the green and blue components. Here, \(f\) is 0 if the surface is facing away from the light and is 1 otherwise. \(f\) is 1 when \(L\cdot N\) is greater than 0, that is, when the angle between \(L\) and \(N\) is less than 90 degrees. When \(f\) is zero, there is no diffuse or specular contribution from the light to the color of the vertex. Note that even when \(f\) is 0, the ambient component of the light can still affect the vertex color.
  • In the equation, \(att\) is the attenuation factor, which represents attenuation of the light intensity due to distance from the light. The value of \(att\) is 1 if the light source is directional. If the light is positional, then \(att\) is computed as \(1/(a+br+cr^2)\), where \(a\), \(b\), and \(c\) are the attenuation constants for the light and \(r\) is the distance from the light source to the vertex. And \(spot\) accounts for spotlights. For directional lights and regular positional lights, \(spot\) is 1. For a spotlight, \(spot\) depends on where the surface point is in the cone of light from the spotlight. (I'll leave the actual formula out here.)
  • The diffuse component of the color, before adjustment by \(f\), \(att\), and \(spot\), is given by \(ld_r*md_r*(L\cdot N)\). This represents the diffuse intensity of the light times the diffuse color of the material, multiplied by the cosine of the angle between \(L\) and \(N\). The angle is involved because for a larger angle, the same amount of energy from the light is spread out over a greater area. As the angle increases from 0 to 90 degrees, the cosine of the angle decreases from 1 to 0, so the larger the angle, the smaller the diffuse color contribution. The specular component, \(ls_r*ms_r*max(0,V\cdot R)^{mh}\), is similar, but here the angle involved is the angle between the reflected ray and the viewer, and the cosine of this angle is raised to the exponent \(mh\). The exponent is the material's shininess property. When this property is 0, there is no dependence on the angle (as long as the angle is greater than 0), and the result is the sort of huge and undesirable specular highlight that we have seen in this case. For positive values of shininess, the specular contribution is maximal when this angle is zero and it decreases as the angle increases. The larger the shininess value, the faster the rate of decrease. The result is that larger shininess values give smaller, sharper specular highlights.
  • Remember that the same calculation is repeated for every enabled light and that the results are combined to give the final vertex color. It's easy, especially when using several lights, to end up with color components larger than one. In the end, before the color is used to color a pixel on the screen, the color components must be clamped to the range zero to one. Values greater than one are replaced by one. It's easy, when using a lot of light, to produce ugly pictures in which large areas are a uniform white because all the color values in those areas exceeded one. All the information that was supposed to be conveyed by the lighting has been lost. The effect is similar to an over-exposed photograph. It can take some work to find appropriate lighting levels to avoid this kind of over-exposure.