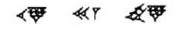Math 110-02, Fall 2008
Some Background on Number Systems

This week's reading from The Math Instinct has a short section on numbers systems, such as Roman numerals and Babylonian number tokens. This handout has some additional information on number systems. There will be a few problems drawn from this material on the next homework assignment.

As the book notes, the first method of keeping track of numbers was probably a tally. In a tally, you simply make one mark or other token for each item that you want to count. The tokens can be pebbles in a pile, notches on a stick, knots in a string, or strokes on paper. With tallies, you don't really have to count at all -- if you put a notch in a stick for each sheep that you send out to pasture, you just have to check whether the sheep still match up one-to-one with the notches when the sheep come home. You don't have to have an abstract number to represent the quantity of sheep.

We still use tallies today, usually by making strokes on paper. It is common to group the strokes into groups of five, as in this illustration:

The idea of grouping strokes leads easily to the idea of replacing a group of strokes with a single symbol. You might use a symbol to represent five or, more commonly, ten items in a tally. In the very earliest number systems, different symbols were used for counting different kinds of objects -- for example, on symbol to represent ten sheep, another to represent ten jars of olive oil, and another to represent ten bushels of wheat. The step from this to using one symbol to represent ten of anything is perhaps the first step towards a truly abstract idea of number.

Of course, once you have a symbol to represent "ten," it's not a big step to come up with another symbol for "ten groups of ten" -- that is a symbol for what we call "one hundred." Add a symbol for "one thousand," another for "ten thousand," and so on for as far as you like to go, and you have a versatile number system that can represent even very large quantities compactly. The Egyptians had such a number system. (Images by Jim Loy.) The symbols in the Egyptian system are shown at the right. Note the symbol for 1,000,000 -- a man with arms raised in wonder. To represent a number such as 1,995, the Egyptians would simply draw as many symbols as necessary: one thousand, nine hundreds, nine tens, and 5 units:

Other ancient cultures used similar systems, but often used letters of the alphabet instead of pictures to represent numbers. As the book mentioned, the Greeks and Romans used such a system. We still use Roman numerals today for some purposes, so a lot of people are familiar with them. In addition to the Greek number system described in the book, the Greeks had a second number system based on their alphabet (the one described in the book was an older system, which was eventually used much like we now use Roman numerals, for ceremonial purposes). In this system, every letter of the Greek alphabet was assigned a value, with individual symbols for 1, 2, 3, ..., 9, 10, 20, 30, ..., 90, 100, 200, ..., 900. The correspondence between letters and numbers is shown in the illustration on the right (taken from here.) (In fact, since the standard Greek alphabet only had 24 characters, they had to add three obsolete letters that were used only for numbers: digamma, koppa, and sampi.)

You can see how this leads to much more compact representations of number than the Egyptian system. Whereas an Egyptian would have to use nineteen symbols to represent 649, a Greek would only need three: χμθ. You might wonder how they would represent numbers larger than 999. For the numbers 1000, 2000, 3000, ..., 9000, they used the same symbols as for 1, 2, 3, ..., 9, but with an iota (ι) added as a superscript or subscript before the letter. Thus, 1000 was represented by ^ια or by _ια; 2000 by ^ιβ or by _ιβ, and so on. This gives a representation for numbers up to 9999. For even bigger numbers, they used notations based on a myriad, or ten-thousand. A given number of ten-thousands was represented by the symbol M, standing for "myriad," with the number of ten-thousands written in the usual way above the M. Thus, 10000, 20000, 30000, ..., 90000, were represented as

Putting all this together, 5413382 could be represented as:

One of the most well-developed of the ancient number systems arose in Babylon some time after the physical token system described in the book. Like our own number system, it was positional. That is, the value represented by a symbol depends on the position of the symbol in the number (like the first "7" in "777" represents 7 hundreds, the second "7" represents 7 tens, and the third represents 7 units). The Babylonian system, however, used groups of sixty instead of groups of ten. Actually, it was based, in a way that looks somewhat peculiar to us, on both the number 10 and the number 60. First of all, the numbers 1 through 59 were represented in much the same way the Egyptians would represent them, using one symbol to represent "one" and another to represent "ten", and simply combining as many of these two basic symbols as necessary:

For larger numbers, the above symbol groups were used in the same way that we use the digits 1, 2, ..., 9. That is, larger numbers are made by stringing groups of symbols from the above table together. In a Babylonian number, the group of symbols on the right represents the number of "units", from 1 times 60 to 59 times 60; the next group over from the right represents the number of "sixties," from 1 to 59; the group after that represents the number of "sixty-squareds" or "three-thousand-six-hundreds"; and so on. For example,

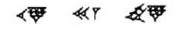
represents 17 times 3600, plus 21 times 60, plus 47, or 62507. One problem that you might have noticed is that the Babylonian system did not originally have a zero. Eventually, they invented a symbol to represent zero, but that is another story, one that we will get to in the next book that we read, ZERO: The Biography of a Dangerous Idea.