This week's assignment has three parts. One part deals with "cut-and-paste topology exercises" similar to what we did in the second half of the class on Monday. The second part is about symmetry groups of patterns in the plane. The third part is to write an outline or plan for your final project. You will have time to work in a group on the first two parts in class (but you should write up your own solutions to turn in). All three parts of the assignment are due in class next Wednesday, April 23.
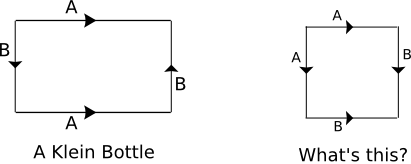
In class on Monday, we saw how the torus and the projective plane can be made by gluing together edges of a rectangle. The edges can be glued together in other patterns as well. This illustration shows the Klein bottle and another 2-manifold that can be created in this way:
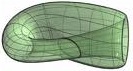A Klein bottle is similar to a torus, in that it can be made from a cylinder. (You get
the cylinder by identifying the sides labeled "A" in the above illustration.) However,
the Klein bottle can't exist in our universe.
It's impossible to join up the ends of
the cylinder without dragging one end through the cylinder and coming up on the other
end from behind. An image of this is shown on the right -- but it's not a real Klein
bottle since it intersects itself. Anyway, you don't have to understand all this
to do the exercises.
Exercise 1: Is a Klein bottle orientable? What happens to an "R" that lives in the Klein bottle and goes on a journey from left to right in the above illustration? What happens to the "R" as it reaches and passes through the edge labeled "B"? Illustrate your answer with a few drawings.
Exercise 2: Use a sequence of drawings to show that a Klein bottle can be made by sewing two Möbius strips together along their edges.
Exercise 3: Identify the 2-manifold that is represented by the figure shown on the right of the above illustration. Explain.
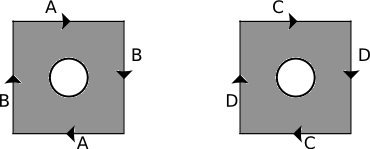
Exercise 4: Suppose that you take two projective planes, and cut out and discard a disk from each one, as shown in the illustration below. Suppose that you then sew the edges of the two holes together. Identify the 2-manifold that is produced by this operation. Explain.
For this part of the lab, you should use information from the reading "About Symmetries of the Plane" to determine the symmetry group of several patterns in the plane.
Exercise 5: Determine the symmetry group for each of the following twelve patterns. (Ignore imperfections in the picture.) In your answer, you can just give the name of the symmetry group. In each case, the symmetry group is either one of the rotation groups or one of the dihedral groups. You don't have to justify your answer unless you want partial credit.
Exercise 6: Here are some pictures of friezes. You should imagine that each pattern extends indefinitely to the left and to the right, and you should ignore imperfections in the pictures. Determine the symmetry group for each pattern. The answer in each case is one of the frieze groups, F1 through F7. Explain your reasoning in each case.
| a) |
b) |
| c) |
d) |
Exercise 7: Here are some pictures of wallpaper patterns. You should imagine that each pattern extends indefinitely in all directions, and you should ignore imperfections in the pictures. Determine the symmetry group for each pattern. The answer in each case is one of the seventeen wallpaper groups. Explain your reasoning in each case.
| a) |
b) |
| c) |
d) |
Exercise 8: Your final project for the course is due on Wednesday, April 30. As mentioned in the handout, I would like you to hand in an outline or plan for your project before then. The outline/plan is Exercise 8 of this lab, and it is due along with the rest of the lab on Wednesday, April 23. If your final project is a paper, you should turn in a one-page outline of the paper, along with a bibliography. No one in the class proposed doing any other type of project, but if you decide that you would like to do something along a different line, then we should discuss your idea and what kind of plan you will turn in next Wednesday.