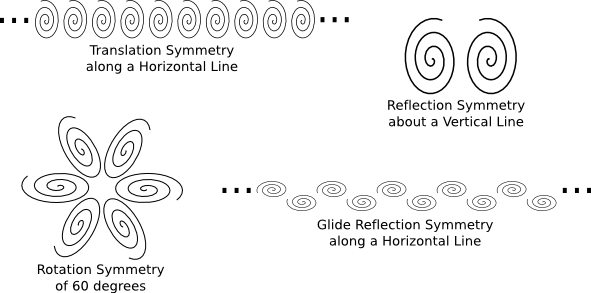
Consider a "repeating pattern" in the plane (a concept that I won't define exactly at this time). To understand what is meant by a symmetry of the pattern, imagine that you've traced the pattern onto a transparent plastic sheet. Now think about moving the sheet to a different position where the tracing on the sheet still matches the pattern. That motion is called a symmetry of the pattern. There are four basic types of symmetry for planar patterns:
Here are some pictures of patterns that display each of these basic types of symmetry:

A pattern can have many symmetries. First of all, a basic symmetry operation can be repeated: If a pattern is symmetric under a rotation of 60 degrees, it is automatically symmetric under a rotation of 2 times 60 degrees, or 3 times 60 degrees, and so on. If a pattern is symmetric under a horizontal translation by 5 inches, it is automatically symmetric under translations of 10 inches, 15 inches, 20 inches, and so on. In fact, we can take two symmetry operations of different types and follow one by the other to get a new symmetry operation. For example, if a pattern is symmetric under a reflection and under a translation, then it is symmetric under the operation "first do the reflection, then do the translation." Furthermore, every symmetry operation has an inverse operation. If you think of a symmetry operation as a motion of the pattern, then the inverse is the opposite motion, the one that returns the pattern to its original position. The inverse of a translation is a translation by the same amount in the opposite direction. The inverse of a rotation is a rotation through the same number of degrees in the opposite direction (clockwise if the original rotation is counterclockwise, and vice versa). The inverse of a reflection operation is itself. To complete the story, we consider the identity operation to be a symmetry operation. The identity operation is to do nothing at all; it is the "motion" that consists of not moving. Of course, the identity is a symmetry for any pattern whatsoever; it would not usually be called a symmetry, but we need it for completeness. Note that if you follow a symmetry operation by its inverse, you get the identity.
All of this amounts to saying that the symmetry operations of a pattern form what mathematicians call a group: If you follow one operation in the group by a second operation in the group, then the combined operation is again in the group. There is an identity operation in the group. And every operation in the group has an inverse operation in the group; when an operation is followed by its inverse, the resulting combined operation is the identity. Group theory is an important field of mathematics, and it is often considered to be the study of symmetry. Group theory can be applied to study the possible symmetry groups of the plane. Let's look at some of the possibilities.
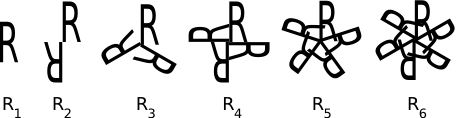
In the first type of symmetry group that we consider, the only symmetries that occur are rotations. (We consider the identity to be a rotation through zero degrees.) This category includes the symmetry groups R1, R2, R3, R4, .... For any positive integer n, Rn is called the rotation group of order n. The subscript n in Rn refers to the number of copies of the basic pattern. The group Rn consists of the rotation through 360/n degrees, plus the rotations that are obtained by repeating this basic rotation up to n times. Note that you get the identity by repeating the basic rotation n times, since rotating by 360 degrees is the same as not rotating at all. After n repetitions, further repetitions of the 360/n degree rotation don't produce anything new.
The following picture shows patterns whose symmetry groups are Rn, for n = 1, 2, 3, 4, 5, and 6. R1 means that there is no symmetry at all (except for the identity, which isn't really a symmetry at all). R2 means that the pattern is symmetric under a 180-degree rotation (plus the identity). For R3, the pattern is symmetric under rotations of 120 and 240 degrees. And so on:
Take the rotation group Rn and add a reflection through a line. Use a line that passes through the center of rotation. Because of the rotational symmetries, you automatically get reflections through other lines -- all the lines that you can get by applying one of the rotations in Rn to the original line of reflection. The resulting group has 2n elements: n reflections and n rotations (counting the identity as a rotation). This group is called the dihedral group of order n. For n greater than 2, the dihedral group Dn is the symmetry group of a regular polygon with n sides. For example, D3 is the symmetry group of an equilateral triangle, and D4 is the symmetry group of a square.
The following picture shows patterns whose symmetry groups are Dn, for n = 1, 2, 3, 4, 5, and 6. Note that the first pattern, for D1 has a single reflectional symmetry and no rotational symmetry. These patterns are obtained by adding a reflection to each of the patterns shown above for the rotation groups:


So far, the symmetry groups that we have encountered have not included any translational symmetries. A frieze group is a symmetry group that contains one basic translation. Every other translation in the group can be obtained by repeating the basic translation or its inverse. (Of course, all these repetitions are automatically in the group; the point is that there is no other, independent translation in the group.) Note that a frieze group is infinite in size, since it contains an infinite number of translations.
It turns out that there are only seven types of frieze group, which are referred to as F1, F2, ..., F7. The different types of frieze group are characterized by the other types of symmetry operations that the group contains, in addition to the translations. The picture at the right shows patterns that have the seven frieze groups as their symmetry groups. You should consider the patterns to be indefinitely extended to the left and to the right. (This picture is from the Wikimedia Commons.)
F1 is the simplest frieze group. It contains no symmetry operations except for the basic translations and the translations obtained by repeating it and its inverse.
F2 contains a glide reflection, but no simple reflections. Note that if you repeat the basic glide reflection, you get a translation, which is the basic translation of the group.
F3 has one reflection, through a line that is parallel to the translation direction. This line is horizontal in the picture. There are no reflections through vertical lines. It also has a glide reflection, but it's included automatically, since it can be obtained by following one operation that is already in the group by another: the basic translation of the group followed by the reflection through the line parallel to the translation direction.
F4 has a reflection through a line that is perpendicular through the translation direction. Once you add one such reflection, you automatically get reflections through an infinite number of other lines, namely the lines that are obtained by applying translations to the original reflection line. In the picture, the reflection lines are vertical, and there is no reflection through any line parallel to the translation direction. There is no glide reflection.
F5 includes a 180-degree rotation. This is the first rotation that we have seen in a frieze group. The only rotation that a frieze group can contain is a rotation through 180 degrees. There are no reflections or glide reflections.
F6 includes a 180-degree rotation and a reflection through a line that is perpendicular to the translation direction. It automatically gets reflections through an infinite number of other lines, as well as a glide reflection. However, there is no reflection through any line parallel to the translation direction.
F7 has reflections through lines both parallel to and perpendicular to the translation direction. It also automatically gets glide reflections and 180-degree rotations. This group represents the maximum amount of symmetry that is possible in a frieze group.
A frieze group contains translations in one direction only. If we allow a translation in a second, independent direction, we get the wallpaper groups. These groups are named after the repeating two-dimensional patterns that are often seen in wallpapers. It turns out that there are only seventeen types of wallpaper group. A wallpaper group has two independent basic translations. Every other translation in the group can be obtained by repetitions of the two basic translations and their inverses. The wallpaper groups differ in the additional symmetry opertations that they contain, in addition to the translations.
The wallpaper groups have names like p1, p2mg, and p6mm. An "m"in the name tells you that the group includes a reflection (or "mirror") symmetry. A "g" indicates that there is a glide reflection in the group. The number in the group tells you the size of the smallest angle among all the rotation symmetries in the group. The only possible angles of rotation for a wallpaper group are 180 degrees (indicated by a "2" in the name), 120 degrees ("3") 90 degrees ("4"), and 60 degrees ("6"). A "1" in the name means that the group does not contain any reflection symmetries.
We have already seen the wallpaper groups illustrated in the Escher Web Sketch program, and I won't give any pictures here. However, you should now have a better appreciation for the different types of symmetries that they can exhibit. For more information and pictures, see the Widipedia&bsp;article on wallpaper groups. Here is a table, excerpted from that article, that can help you to recognize the wallpaper group of symmeries for a repeating pattern in the plane:
| Least rotation |
Has reflection? | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yes | No | ||||||||||||||||
| 60 degrees | p6m | p6 | |||||||||||||||
| 90 degrees |
|
p4 | |||||||||||||||
| 120 degrees |
|
p3 | |||||||||||||||
| 180 degrees |
|
|
|||||||||||||||
| none |
|
|
|||||||||||||||