Math 130-03, Lab 12

This lab is a review for the test that is coming up tomorrow, April 20. There is no lab report to turn in. An answer sheet will be available at the lab.


1. Compute the following derivatives:


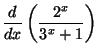
(a) $ \displaystyle \frac{d}{dx} \left(\frac{2^x}{3^x+1}\right)$


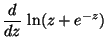
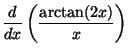
(b) $ \displaystyle \frac{d}{dz}\, \ln(z+e^{-z})$


(c) $ \displaystyle \frac{d}{dx} \left(\frac{\arctan(2x)}{x}\right)$


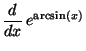
(d) $ \displaystyle \frac{d}{dx}\, e^{\arcsin(x)}$


2. Explain why the function $ g(x)=(x-2)^2+1$ does not have an inverse. Find the inverse of the function $ f(x)=(x-2)^2+1$, $ x\ge2$.


3. Solve the equation $ \ln(3x-1)=1$ for $ x$.


4. Let $ f(x) = xe^x$. Determine whether $ f$ is concave up at $ x=-3$ or concave down. (Don't just look at a graph. Show your work.)


5. Let $ f(x)=2+12x+3x^2-2x^3$. Determine where $ f$ is increasing and where it is decreasing. Determine where $ f$ is concave up and where it is concave down. Show your work.


6. A rocket takes off straight into the sky. An observation post is located one mile (5280 feet) from the launch pad. A few moments after take-off, the rocket is 2000 feet high and is traveling at 500 feet per second. How fast is the distance from the observation post to the rocket increasing at that time?


7. An equilateral triangle with side $ s$ has area $ A=\frac{\sqrt{3}}{4}\cdot s^2$. Suppose that at a certain time, the side of the triangle is 15 inches long and is decreasing at a rate of 3 inches per minute. How fast is the area changing at that time?


8. Sand is pouring from a spout at the rate of 3 cubic feet per minute and is falling on on a conical pile whose diameter is always three times the height. At what rate is the height increasing at the time when the height is 4 feet? (Recall that the volume of a cone with radius $ r$ and height $ h$ is given by $ V=\frac{1}{3}\pi r^2h$.)


9. Draw a sketch of a curve which satisfies the following properties:

a) $ f'(x)>0$ for all $ x$

b) $ f''(x)>0$ for $ x<1$ and $ f''(x)<0$ for $ x>1$

c) $ f(1)=1$

d) $ \displaystyle \lim_{x\to-\infty}f(x)=0$ and $ \displaystyle \lim_{x\to\infty}f(x)=2$


10. Draw a sketch of a curve which satisfies the following properties:

a) $ f$ has points of inflection at $ (-1,2)$ and $ (1,2)$ and at no other points.

b) $ f$ has horizontal tangent lines at $ (-2,3)$, $ (0,0)$, and $ (2,3)$ and at no other points.

c) Both $ f'(x)$ and $ f''(x)$ are defined for all $ x$.


11. Let $ f$ be the function whose graph is shown below. State where $ f$ is concave up, where it is concave down, where it is increasing, where it is decreasing. Find any points of inflection. Your answers might be approximate.

(Graph omitted -- you get the idea.)


12. Since the second derivative of a function is the derivative of the first derivative, we have that

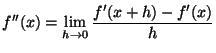
$\displaystyle f''(x)=\lim_{h\to0}\frac{f'(x+h)-f'(x)}{h}$

Use this fact to find a numerical estimate for $ f''(-1)$ and for $ f''(1)$, where $ f$ is the function with the following graph:

(Graph omitted -- you get the idea.)



David Eck, April 2001