Math 130-03, Lab 3

Practice Problems


Here are some limit calculations for you to try. (These problems are not to be turned in.)

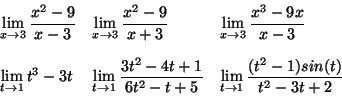
\begin{displaymath} \begin{array}{lll} \displaystyle \lim_{x\to3}\frac{x^2-9}{x... ...& \displaystyle \lim_{t\to1}\frac{t^3-1}{t^2-2t+1} \end{array}\end{displaymath}




Lab Report Problems


Exercise 1 The following applet can display several example functions. To load one of the examples, select it from the menu at the top of the applet, then click the "Load Example" button. For each example, find the value of each of the following limits, or explain why the limit does not exist:

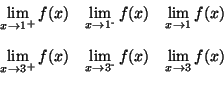
\begin{displaymath} \begin{array}{lll} \displaystyle \lim_{x\to 1^+}f(x)& \di... ... 3^\text{-}}f(x)& \displaystyle \lim_{x\to 3}f(x) \end{array}\end{displaymath}

You can examine the value of the function at different x-values by moving the slider or by typing a number in the input box at the bottom of the applet. Note that you can zoom in on a point by clicking there, and you can zoom out from a point by holding down the shift key and clicking there. In the lab report, explain how you used the applet to get your answers.



Exercise 2 We first looked as limits as a way of finding the slope of a tangent line. The slope of a tangent line is given as a limit of slopes of secant lines. Here is an applet that shows a tangent line and a secant line to a given graph. The slope of the secant line is shown in the corner of the applet. You can adjust the point where the tangent line is drawn by dragging the red dot or by typing an x-coordinate in the box labeled "Tangent at x =". The secant line extends from the same point to another point shown as a green dot. You can adjust the secant line by dragging the green dot or by typing an x-coordinate into the box labeled "Secant to x =". To change the function that is being graphed, just type the formula in the box labeled "f(x) =" and press return. See what happens as you move the green dot closer to the red dot. Note that you can also click-and-drag with the right mouse button to slide the whole graph around.

Use this applet to investigate the following. (In part (d), the tangent line actually does not exist! The applet gets this wrong. Never trust a computer.)

(a) the slope of the tangent line to $ y=sqrt(x)$ at the point where $ x=1$

(b) the slope of the tangent line to $ y=x^3-2*x+1$ at the point where $ x=0$

(c) the slope of the tangent line to $ y=2^x+cos(x)$ at the point where $ x=1$

(d) the slope of the tangent line to $ y=abs(x)$ at the point where $ x=0$


In your lab report, give your estimates for the slopes in parts (a), (b), and (c), and explain how you got your answers. For part (d), explain why the specified tangent line really does not exist. (Remember that for a limit to exist, both the left-hand limit and the right-hand limit must exist, and they must be equal.)



Exercise 3 (This is the exercise that we skipped last week, with a slightly modified applet.) The next little program (or ``applet'') that you will look at is an applet that should help you understand composition of functions. Given two functions $ y=f(x)$ and $ y=g(x)$, this applet shows the graph of $ y=g(f(x))$. There is a small red square on the x-axis in the graph of $ f$. You can drag this square back and forth, and the applet marks the corresponding points on the graphs. Click the button to launch the applet:

For the program that you are using in this course, the absolute value function should be written as abs(x) rather than |x|. If $ y=h(x)$ is any function, we can form the composition functions $ y=abs(h(x))$ and $ y=h(abs(x))$. Use the Composition Applet to look at these compositions for the function $ sin(x).$ That is, you want to consider the compositions $ y=abs(sin(x))$ and $ y=sin(abs(x)).$ To work with $ y=abs(sin(x))$, set up the applet with $ f(x)=sin(x)$ and $ g(x)=abs(x)$. Drag the red square back and forth to help you understand how the graph of $ abs(sin(x))$ is created. Then reverse the definitions of $ f(x)$ and $ g(x)$ to work with $ sin(abs(x))$.


Here is what you should do to turn in:


(a) Sketch the graphs of $ abs(sin(x))$ and $ sin(abs(x))$, and explain why the graphs have the shapes they do.

(b) Suppose that $ h$ is any function. Explain in words how the graph of $ y=abs(h(x))$ can be obtained from the graph of $ y=h(x)$. (Of course, you could obtain the graph by plotting points. But I want a simple geometric construction that will make the graph of $ y=abs(h(x))$ from the graph of $ y=h(x)$.) You can use the applet to help you think about this by looking at different functions.

(c) Suppose that $ h$ is any function. Explain in words how the graph of $ y=h(abs(x))$ can be obtained from the graph of $ y=h(x)$. (Again, give a geometric description.)