Math 130-03, Lab 4


Practice Problems

There is a test tomorrow (Friday, February 16). In lab, I will hand out a set of review problems for the test for you to work on. I hope that the two exercises for the fourth lab report will only take up part of the lab.


Exercise 1

According to the epsilon/delta definition, $ \displaystyle \lim_{x\to a}f(x)=L$ if for each positive number, $ \varepsilon$, it is possible to find a positive number, $ \delta$, such that whenever $ x$ is a number with $ 0<\vert x-a\vert<\delta$, it will also be true that $ f$ is defined at $ x$ and $ \vert f(x)-L\vert<\varepsilon$.

In the applet shown below, the graph of a function, f(x), is shown, and numbers a and L have been picked for you. You can change the values of epsilon and delta by dragging the sliders at the bottom of the applet or by typing new numbers into the input boxes. On the graph, a green line represents the vertical line $ x=a$, and a red line represents the horizontal line $ y=L$. The pink area, together with the yellow area, consists of the points $ (x,y)$ for which $ \vert y-L\vert<\varepsilon$. The light green area, together with the yellow area, consists of the points $ (x,y)$ for which $ \vert x-a\vert<\delta$. You can vary the widths of these regions by changing the values of epsilon and delta. The graph of the function is shown in black.

What has to be true in this applet if the limit of f(x) as x approaches a is in fact equal to L? It means that you can set the epsilon slider to any value you like, except zero. Then, no matter what positive epsilon you've chosen, it must be possible to adjust the delta slider so that the graph passes through the yellow region without straying into the green region. (A point $ (x,f(x))$ in the green region represents a value of $ x$ such that $ \vert x-a\vert<\delta$ but $ \vert f(x)-L\vert\ge\epsilon$. This is bad.) Note that if epsilon is made smaller, then delta might also have to be made smaller. If the limit is L, you will always be able to make delta small enough to work. If you encounter an epsilon for which no value of delta will work, then the limit is not equal to L. (The limit could still exist, if it's equal to some other value than L.)

In the example that is shown when the applet first starts up, the delta value is too big for the epsilon that is selected. The graph hits the green area. However, a smaller value of delta will work. Change delta to 0.1, for example. To get a better view, you can zoom in on a point by clicking on it. Click on the point $ (a,L)$ two or three times. (This is the point where the red and green lines intersect.) This will enlarge the graph nicely.

Now, try a smaller value of epsilon. Set epsilon to 0.1. The value delta = 0.1 is now too big. But if you reduce it, say to delta = 0.04, it works again. If you reduce epsilon again, you might be forced to reduce delta, and so on. If this process can be repeated infinitely - no matter how small epsilon is, you can find a delta - then the limit as x approaches a is L. If you ever get stuck - if you find a positive epsilon for which no positive delta works - then the limit as x approaches a is not L. On a computer, of course, you can't really repeat this process infinitely, since the computer can't deal with arbitrarily small numbers. But it can help you understand what is going on.


Before going on to the exercise, make sure that you understand the startup example:

Now, for the stuff that you need to turn in. Besides the startup example, the applet contains four other examples. To load one of the examples, select it from the pop-up menu at the top of the applet and click the "Load Example" button. For each example, look at what happens for $ \varepsilon$ = 0.1, 0.01, and 0.001. For each value of $ \varepsilon$, see if you can find a value of $ \delta$ such that for every $ x$ with $ 0<\vert x-a\vert<\delta$, it follows that $ \vert f(x)-L\vert<\varepsilon$. Report your results (including the numerical value of each $ \delta$, if you can find one that works). For each example, carefully state what you can conclude about $ \displaystyle \lim_{x\to a}f(x)$ and why.

Don't forget that you can click at a point to zoom in on it!



Exercise 2

The last example in the previous exercise was the limit of the function x*sin(1/x). This function has a limit as $ x$ approaches 0, but it is not defined at 0. For the split function

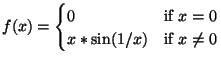
$\displaystyle f(x)=\begin{cases}0 &\hbox{if $x=0$}\\ x*\sin(1/x) &\hbox{if $x \ne 0$} \end{cases}$

the limit of $ f(x)$ as $ x$ approaches 0 is $ f(0)$. Now, we can ask whether this function has a tangent line at $ x=0$. Check it out with the applet below. (The funny-looking function definition, (x = 0)? 0 : x*sin(1/x), is just a way of writing the above split function. It means ``if x = 0, then the value is 0, otherwise the value is x*sin(1/x).'' This is a notation that can be used in all the applets that you encounter in this course.) The applet is the same one that you used in the previous lab to work with secant lines and tangent lines.

For this exercise, investigate the limit of the secant line between (0,0) and the point $ (x,f(x))$ on the graph of this function, as $ x$ approaches 0. Note that this function is very badly behaved near 0, and the applet does not do a great job of drawing the graph. And the fact that the applet draws a red ``tangent line'' does not necessarily mean that the tangent line really exists. Try zooming in on the graph to get a closer look. Use the ``Zoom In'' button to zoom.

Now, try changing the function to: (x = 0)? 0 : (x*x)*sin(1/x), and investigate the limit of the secant line between (0,0) and the point $ (x,f(x))$ on the graph of this function, as $ x$ approaches 0. Try zooming in on the graph to get a closer look. Use the ``Zoom In'' button to zoom.

Report on your results in both cases. Do you think the tangent line exists? Why or why not? If it exists, what is its slope?


David Eck, February 2001