Math 130-03, Lab 5


This lab is mostly about continuity. Only one exercise uses the computer. For the other two exercises, you should definitely work with one or two partners. The first exercise, especially, requires discussion.


Exercise 1


The instructions for Form 1040 (Federal Income Tax) gives the following table for computing the amount of tax, based on your taxable income. (This is the table for use by a single taxpayer).


If income is over But not over Then tax is of amount over
$0 $26,250 15% $0
26,250 63,550 $3,937.50 + 28% 26,250
63,550 132,600 $14,381.50 + 31% 63,550
132,600 288,350 $35,787.00 + 36% 132,600
288,350   $91,857.00 + 39.6% 288,350


(a) Use more standard mathematical notation to write the amount of tax as a function of the income. For example, T(x) = 3937.50 + 0.28*(x-26250) if 26250 < x <= 63550. (Use "split function" notation.)

(b) Is tax a continuous function of income? Explain your answer.

(c) Consider the question of what would make a tax system ``fair.'' In a fair tax system, should tax necessarily be a continuous function of income? If so, why is this condition necessary to a fair system? If not, why is it unnecessary? This is a discussion question. I expect to return to this question of ``fairness'' in a later lab.



Exercise 2


In class, we discussed how the Intermediate Value Theorem can be used to find a zero of a function: If $ f$ is a continuous function and $ a$ and $ b$ are numbers such that $ f(a)$ and $ f(b)$ have opposite sign, then there is a number $ c$ between $ a$ and $ b$ such that $ f(c)=0$. In practical terms, this means that if you see a continuous function cross the x-axis, you can be sure that it actually hits the x-axis. The point where it crosses the x-axis is a zero of the function.

You can find an approximate value for a zero of a function by zooming in on the point where it crosses the x-axis. In the following applet, you can zoom in on a point by clicking on that point or by drawing a box around that point. You can also right-click and drag the graph to slide it around.

Use this applet to find each of the following values to at least four decimal places. In each case, find a function that has the given value as a zero. (In part (a), for example, the square root of two is a zero of the function $ f(x)=x^2-2$.) Graph the function, and zoom in on the point where the graph crosses the x-axis until you can find the x-coordinate of the crossing point to the desired accuracy.


(a) Find the value of $ \sqrt{2\,}$

(b) Find the value of $ \root 3 \of {5\,}$

(c) Find a number $ x$ such that $ x=\cos(x)$



Exercise 3


The functions that you are familiar with are continuous everywhere they are defined, except possibly for a few isolated points. Is this true for all functions, or are there functions that are discontinuous at most or even all of the points where they are defined? What would the graph of such a function look like? This exercise gives a famous example of such a function.

Recall that a real number $ x$ is said to be rational if it can be written in the form $ n/m$, where $ n$ and $ m$ are integers. A number that cannot be written in this form is said to be irrational. A basic fact about the real numbers is that every open interval, no matter how small, contains both rational and irrational numbers. Put another way, given any real numbers $ a$ and $ b$, there are both rational and irrational numbers between $ a$ and $ b$. Consider the following function:

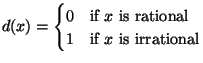
$\displaystyle d(x)=\begin{cases}0&\text{if $x$ is rational}\\ 1&\text{if $x$ is irrational}\end{cases}$

The function $ d$ is defined for every real number $ x$, but it is not continuous at any point. Explain why this is true. Try to give a formal explanation that uses the epsilon/delta definition of limit, but if you can't do that, just give an informal explanation. What would the graph $ y=d(x)$ look like? Is it possible to draw this graph?

(The function $ d$ is called the Dirichlet function, after the mathematician who discovered it. Mathematicians call examples like this one, which have behaviors that seem bizarre, pathological examples. In mathematics, pathological examples are an important tool for understanding, since they show ways in which ``common-sense'' expectations can go wrong in the world of mathematics.)


David Eck, February 2001