A Short Introduction to Metric Spaces
Section 2: Subspaces and Product Spaces
One of the things that we can do with metric spaces is to make "new spaces from old." For example, a subset of a metric space can be made into a metric space in its own right in a natural way. And given two metric spaces, their cross product can be made into a metric space; in fact, there are several reasonable ways to do that. This section looks at subspaces and products of metric spaces. The material on subspaces will be needed in later sections of this web site. The material on product spaces, although interesting, will not be needed and can be skipped.
Subspaces
It should be clear that if $(M,d)$ is a metric space, then a subset of $M$ can be made into a metric space by using the same measure of distance on the subset as is used on $M.$ The subset with that inherited metric is called a "subspace."
Definition 2.1: Let $(M,d)$ be a metric space, and let $X$ be a subset of $M.$ We define a metric $d'$ on $X$ by $d'(x,y)=d(x,y)$ for $x,y\in X.$ Then $(X,d')$ is a metric space, which is said to be a subspace of $(M,d).$
The metric $d'\colon X\times X\to \R$ is just the function $d$ restricted to the subset $X\times X$ of $M\times M.$ In practice, we will often use the same name for the distance function on a subspace as is used for the distance function on the containing space, but in this section, for clarity, I will avoid doing that.
A big part of understanding a metric space is understanding its open sets and closed sets. To understand a subspace $(X,d')$ of $(M,d)$, we can start by noting that for $x\in X$, the open ball $B_r^{d'}(x)$ in $(X,d')$ is just the intersection with $X$ of the corresponding open ball in $(M,d)$. That is, $B_r^{d'}(x) = B_r^d(x)\cap X$. This is clear because for $y\in X$, $d(x,y) = d'(x,y)$ and therefore $d'(x,y)<r$ if and only if $d(x,y)<r$. In fact, we get the following similar characterization for all open and closed sets in $(X,d')$.
Theorem 2.1: Let $(M,d)$ be a metric space and $X$ a subset of $M,$ and let $d'$ be the subspace metric on $X.$ A subset $U$ of $X$ is open in the subspace $(X,d')$ if and only if there is an open subset $\mathcal O$ of $M$ such that $U=X\cap \mathcal O.$ A subset $F$ of $X$ is closed in the subspace $(X,d)$ if and only if there is a closed subset $\mathcal C$ of $M$ such that $F=X\cap \mathcal C.$
Proof: Suppose that $U$ is an open subset in the subspace $(X,d').$ For every $u\in U,$ there is an $\epsilon_u>0$ such that $B_{\epsilon_u}^{d'}(u)\subseteq U.$ Let $\mathcal O$ be the union of the corresponding open balls in $M$. That is, $\mathcal O = \bigcup_{u\in U}B_{\epsilon_u}^d(u).$ Note that $\mathcal O$ is an open subset of $M$ because it is a union of open balls in $M.$ We have $$\begin{align*} X\cap \mathcal O &= X\cap\left(\bigcup_{u\in U}B_{\epsilon_u}^d(u)\right)\\ &= \bigcup_{u\in U}\big(X\cap B_{\epsilon_u}^d(u)\big), \text{by the distributive law} \\ &= \bigcup_{u\in U} B_{\epsilon_u}^{d'}(u)\\ &= U \end{align*}$$ The last equality follows since $B_{\epsilon_u}^{d'}(u)\subseteq U$ for all $u,$ and their union includes every $u\in U$ because $u\in B_{\epsilon_u}^{d'}(u).$
Conversely, Suppose that $\mathcal O$ is an open subset of $M,$ and let $U = X\cap\mathcal O.$ We must show that $U$ is open in $(X,d').$ Let $u\in U.$ We need to find $\epsilon>0$ such that $B_\epsilon^{d'}(u)\subseteq U.$ Since $u\in \mathcal O$ and $\mathcal O$ is open in $M,$ there is an $\epsilon>0$ such that $B_\epsilon^d(u)\subseteq\mathcal O.$ But then $B_\epsilon^{d'}(u) = X\cap B_\epsilon^d(u) \subseteq X\cap \mathcal O = U.$ That is, $B_\epsilon^{d'}(u)\subseteq U.$
Turning to the case of closed subsets, note first that for a subset $A$ of $M$ and a subset $B$ of $X,$ $X\cap A = X\smallsetminus B$ if and only if $X\cap (M\smallsetminus A)= B.$ So, applying the first part of the theorem,
| $F$ is closed in $X$ | $\Longleftrightarrow$ $X\smallsetminus F$ is open in $X$ |
| $\Longleftrightarrow$ $X\smallsetminus F = X\cap \mathcal O$, for some open $\mathcal O \subseteq M$ | |
| $\Longleftrightarrow$ $F=X\cap(M\smallsetminus \mathcal O)$, for some open $\mathcal O \subseteq M$ | |
| $\Longleftrightarrow$ $F= X\cap \mathcal C$, for some closed $\mathcal C\subseteq M$ |
and that completes the proof. ∎
As an example, we can make the set of rational numbers, $\Q$, into a metric space $(\Q,d')$ using the subspace metric inherited from $(R,d)$. Let $A=\{x\in\Q\,|\,-\sqrt{2} < x < \sqrt{2}\}.$ Then $A$ is the intersection with $\Q$ of the open interval $(-\sqrt{2},\sqrt{2}\,)$, which is an open set in $(\R,d)$. By the theorem, $A$ is open in $(\Q,d').$ But since $\sqrt{2}$ is not a rational number, $A$ is also a closed set in $(\Q,d')$ because $A=\Q\cap[-\sqrt{2},\sqrt{2}].$ There are many subsets of $\Q$ that are both open and closed in $(\Q,d')$. On the other hand, it can be shown that the only subsets of $\R$ that are both open an closed in $(\R,d)$ are $\varnothing$ and $\R.$ (These facts will become significant have we have defined connected sets.)
It might also be instructive to note that $[1,2)$ is an open subset of the subspace $([1,3],d')$ of $(\R,d),$ even though it is not an open set in $(\R,d).$ You are asked to verify this in one of the exercises in this section.
Product Spaces
$\R^2$ is the cross product $\R\times\R$. The usual metric on $\R^2$ can be defined in terms of the metric on $\R$. The usual distance, $\rho,$ between the points $\langle x_1,y_1 \rangle$ and $\langle x_2,y_2 \rangle$ of $\R^2$ is given by $$\rho(\langle x_1,y_1 \rangle,\langle x_2,y_2 \rangle) = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} = \sqrt{d(x_1,x_2)^2+d(y_1,y_2)^2}.$$ This can be generalized to the cross product of any two metric spaces, $(M_1,d_1)$ and $(M_2,d_2)$. That is, we can define a metric space $(M_1\times M_2,\rho)$ where $$\rho(\langle x_1,y_1 \rangle,\langle x_2,y_2 \rangle) = \sqrt{d_1(x_1,x_2)^2+d_2(y_1,y_2)^2}$$ for any $x_1,x_2\in M_1$ and $y_1,y_2 \in M_2.$ However, $\rho$ is not the only natural metric on $M_1\times M_2$, In particular, we can define two alternative metric spaces $(M_1\times M_2,\mu)$ and $(M_1\times M_2,\sigma)$ by $$\begin{align*} \mu(\langle x_1,y_1 \rangle,\langle x_2,y_2 \rangle) &= \max(d_1(x_1,x_2),d_2(y_1,y_2))\\ \sigma(\langle x_1,y_1 \rangle,\langle x_2,y_2 \rangle) &= d_1(x_1,x_2) + d_2(y_1,y_2) \end{align*}$$
This illustration shows the open balls of radius $\varepsilon$ about a point $a\in\R^2$ for each of the three product spaces $(\R^2,\rho)$, $(\R^2,\mu)$, and $(\R^2,\sigma)$:
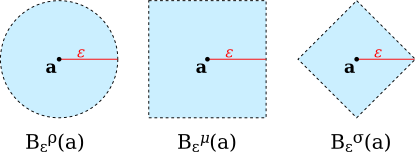
(However, I should note that all three metrics have the same open sets. That is, they produce the same topology on $M_1\times M_2$.)
We should prove that $\rho$, $\mu$, and $\sigma$ are in fact metrics on $M_1\times M_2$. I will leave $\mu$ and $\sigma$ as exercises, but here is a proof for $\rho.$
Theorem 2.2: Suppose that $(M_1,d_1)$ and $(M_2,d_2)$ are metric spaces. Define the function $\rho\colon (M_1\times M_2)\times (M_1\times M_2)\to \R$ by $\rho(\langle x_1,y_1 \rangle,\langle x_2,y_2 \rangle) = \sqrt{d_1(x_1,x_2)^2+d_2(y_1,y_2)^2}.$ Then $\rho$ is a metric on $M_1\times M_2$.
Proof: We need to show that $\rho$ satisfies the three properties that define a metric space. The proofs for the first two properties are straightforward: For property 1, $\rho(\langle x_1,y_1 \rangle,\langle x_2,y_2 \rangle) \ge 0$ for all $\langle x_1,y_1 \rangle$ and $\langle x_2,y_2 \rangle$ because a square root is always non-negative. And $\sqrt{d_1(x_1,x_2)^2+d_2(y_1,y_2)^2} = 0$ if and only if $d_1(x_1,x_2)= 0$ and $d_2(y_1,y_2)=0$, which is in turn true if and only if $x_1=x_2$ and $y_1=y_2$ because $d_1$ and $d_2$ are metrics. Finally, $x_1=x_2$ and $y_1=y_2$ if and only if $\langle x_1,y_1 \rangle =\langle x_2,y_2 \rangle$ by the definition of equality of ordered pairs. For property 2, the symmetry of $\rho$ follows immediately from the symmetry of $d_1$ and $d_2.$
To prove property 3 for $\rho$, let $\langle x_1,y_1 \rangle$, $\langle x_2,y_2 \rangle$ and $\langle x_3,y_3 \rangle$ be elements of $M_1\times M_2$. From the triangle inequality for $d_1$, we know that $d_1(x_1,x_3)\le d_1(x_1,x_2) + d_1(x_2,x_3).$ Squaring both sides, we get $$\begin{align*} d_1(x_1,x_3)^2 &\le (d_1(x_1,x_2) + d_1(x_2,x_3))^2\\ &= d_1(x_1,x_2)^2 + 2d_1(x_1,x_2)d_1(x_2,x_3) + d_1(x_2,x_3)^2\\ &\le d_1(x_1,x_2)^2+ d_1(x_2,x_3)^2 \end{align*}$$ and similarly for $d_2,$ $$d_2(y_1,y_3)^2 \le (d_2(y_1,y_2)^2 + d_2(y_2,y_3))^2$$ Adding these two inequalities and taking the square root gives $$\begin{align*} \rho(&\langle x_1,y_1 \rangle, \langle x_3,y_3 \rangle)\\ &=\sqrt{d_1(x_1,x_3)^2+d_2(y_1,y_3)^2}\\ &\le \sqrt{\big( d_1(x_1,x_2)^2+ d_1(x_2,x_3)^2 \big) + \big( (d_2(y_1,y_2) + d_2(y_2,y_3))^2 \big)}\\ &= \sqrt{\big( d_1(x_1,x_2)^2+ d_2(y_1,y_2)^2 \big) + \big( (d_1(x_2,x_3)^2 + d_2(y_2,y_3))^2 \big)}\\ &\le \sqrt{ d_1(x_1,x_2)^2+ d_2(y_1,y_2)^2} +\sqrt{ (d_1(x_2,x_3)^2 + d_2(y_2,y_3))^2 }\tag{**}\\ &=\rho( \langle x_1,y_1 \rangle, \langle x_2,y_2 \rangle) + \rho(\langle x_2,y_2 \rangle,\langle x_3,y_3 \rangle) \end{align*}$$ which is the triangle inequality for $\rho$. (The inequality (**) follows because for any non-negative numbers $a$ and $b$, $\sqrt{a+b} \le \sqrt{a +2\sqrt{a}\sqrt{b}+ b} =\sqrt{(\sqrt{a}+\sqrt{b})^2}=\sqrt{a}+\sqrt{b}$.) ∎
Of course, it is possible to define metrics on cross products of more than two metric spaces. For example, if $(M_1,d_1)$, $(M_2,d_2)$, $\dots, (M_n,d_n)$ are metric spaces, we can define the metric $\rho$ on $M_1\times M_2 \times \cdots \times M_n$ by $$\rho(\vec{x}{n},\vec{y}{n})=\sqrt{d_1(x_1,y_1)^2+d_2(x_2,y_2)^2+\cdots+d_n(x_n,y_n)^2}$$ The fact that this is a metric for all $n\ge2$ can be proved by induction, noting that $$\begin{align*} &\sqrt{d_1(x_1,y_1)^2+d_2(x_2,y_2)^2+\cdots+d_n(x_n,y_n)^2}\\ &=\sqrt{\Big(\sqrt{d_1(x_1,y_1)^2+d_2(x_2,y_2)^2+\cdots+d_{n-1}(x_{n-1},y_{n-1}n)^2}\;\Big)^2 + d_n(x_n,y_n)^2} \end{align*}$$ This definition, of course, gives us the usual metric on $\R^n.$ The metrics $\mu$ and $\sigma$ on $M_1\times M_2$ can similarly be extended to metrics on $M_1\times M_2 \times \cdots \times M_n$.
Exercises
Exercise 2.1: Consider the closed interval $[1,3]$ as a subspace of $(\R,d)$. Verify that $[1,2)$ is an open set in the subspace $([1,3],d')$.
Exercise 2.2: Let $U$ be an open subset of the metric space $(M,d)$. Show that a subset $A$ of $U$ is an open set in the subspace $(U,d')$ if and only if $A$ is an open set in the space $(M,d).$ (The previous exercise shows that the fact that $U$ is open is essential here.) State and prove a similar result for closed subsets.
Exercise 2.3: Let $\Z$ be the set of all integers, and consider the subspace $(\Z,d')$ of $(\R,d)$. What are the open sets in $(\Z,d')$? How does the metric space $(\Z,d'$) compare to the metric space $(\Z,\delta),$ where $\delta$ is the discrete metric, as defined in Exercise 1.5?
Exercise 2.4: Let $(M_1,d_1)$ and $(M_2,d_2)$ be metric spaces, and consider the metric space $(M_1\times M_2,\rho)$ where $\rho(\langle x_1,y_1 \rangle,\langle x_2,y_2 \rangle) = \sqrt{d_1(x_1,x_2)^2+d_2(y_1,y_2)^2}.$ Suppose that $U_1$ is an open set in $(M_1,d_1)$ and $U_2$ is an open set in $(M_2,d_2)$. Show that $U_1\times U_2$ is an open set in $(M_1\times M_2,\rho).$ Is every open subset of $(M_1\times M_2,\rho)$ of this form?
Exercise 2.5: Explain why the pictures are correct in the illustration in this section of the open balls $B_\varepsilon^\mu(a)$ and $B_\varepsilon^\sigma(a)$ in $\R^2$.
Exercise 2.6: Let $(M_1,d_1)$ and $(M_2,d_2)$ be metric spaces and let $\sigma$ be the metric on $M_1\times M_2$ defined as $\sigma(\langle x_1,y_1 \rangle, \langle x_2,y_2 \rangle)= d_1(x_1,x_2)+d_2(y_1,y_2)$. Show that $\sigma$ is in fact a metric.