Section 13.2
Fancier Graphics
We have seen many examples of using a GraphicsContext to draw on a Canvas. But GraphicsContext has many features besides those that have already been covered. This section continues our study of canvas graphics. We begin by looking at two methods that can be useful for managing the state of a graphics context.
A GraphicsContext, g, has various properties, such as fill color and line width, that affect any drawing done with g. It's important to remember that a canvas has only one graphics context, and any changes made to a property of the graphics context will carry over to all future drawing, until the value of the property is changed again. In particular, changes are not restricted to the subroutine in which they are made. It often happens that a programmer wants to change the value of some properties temporarily and then restore them to their previous values. The graphics API includes methods g.save() and g.restore() that makes this easy. When g.save() is executed, the current state of the graphics context, g, is stored. The state includes almost all of the properties that affect drawing. In fact, the graphics context keeps a stack of states (see Subsection 9.3.1), and g.save() pushes the current state onto that stack. A call to g.restore() pops the top state from the stack, and sets the values of all properties to match their saved values.
Because they use a stack, it is possible to call save() several times before calling restore(). Every call to save() should be matched, eventually, by a call to restore(). (However, unmatched calls to restore() will not produce an error; the extra calls are simply ignored.) An easy way to make sure that changes made to a graphics context in one subroutine do not carry over to future subroutine calls is to call save() at the beginning of the subroutine and restore() at the end.
Save and restore are particularly useful when working with transforms, which are covered later in this section.
13.2.1 Fancier Strokes
We have seen how to stroke lines and curves and even the outlines of text characters, and how to set the color and line width that are used for the stroke. Strokes have other properties that affect their appearance. It is possible to draw strokes that are dotted or dashed instead of solid. And you can control what happens at the endpoints of a stroke, and at the "join" between two lines or curves that meet at a point, such as two sides of a rectangle meeting at one of the corners of the rectangle. A graphics context has properties to control all of these features. You need to be working with fairly wide lines for the endpoint and join properties to have any visual effect. This illustration shows the available options:
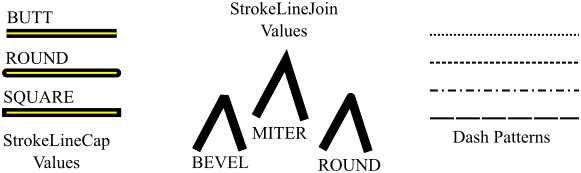
The endpoints of the three line segments on the left show the three possible styles of line "cap." The stroke is shown in black, and the geometric line is indicated by a yellow line down the center of the stroke. In the BUTT cap style, the stroke is simply cut off at the end of the geometric line. For the ROUND cap, a disk is added at the endpoint, with a diameter equal to the line width. For the SQUARE cap, a square is added instead of a disk. The round or square style is what you would get if you draw a stroke with a physical pen that has a round or square tip.
In a graphics context, g, the cap style for strokes is set by calling g.setLineCap(cap). The parameter is of type StrokeLineCap, an enumerated type in package javafx.scene.shape whose possible values are StrokeLineCap.BUTT, StrokeLineCap.ROUND, and StrokeLineCap.SQUARE. The default style is SQUARE.
Line joins are similar. The appearance of a vertex where two lines or curves meet is set by calling g.setLineJoin(join). The parameter is of type StrokeLineJoin, and the possible values are StrokeLineJoin.MITER, StrokeLineJoin.ROUND, and StrokeLineJoin.BEVEL. The three styles are shown in the middle section of the above illustration. The default join style is MITER. In the miter style, the two line segments are continued to make a sharp point. In the other two styles, the corner is cut off; for bevel, it is cut off by a line segment, and for round it is cut off by an arc of a circle. I have found that round joins can look better if you draw a wide curve as a sequence of short line segments.
Dotted and dashed strokes can be made by setting a dash pattern, using the method g.setLineDashes(). The parameters to this method specify the lengths of the dashes and of the gaps between them:
g.setLineDashes( dash1, gap1, dash2, gap2, . . . );
The parameters are of type double (and could also be given as a single array of type double[]). If a stroke is drawn when this dash pattern is in effect, the curve consists of a line or curve of length dash1, followed by a gap of length gap1, followed by a line or curve of length dash2, and so on. The pattern of dashes and gaps will be repeated as often as necessary to cover the full length of the stroke.
For example, g.setLineDashes(5,5) draws a stroke as series of segments of length 5 followed by gaps of length 5, while g.setLineDashes(10,2) produces a series of long segments separated by short gaps. A pattern of dashes and dots could be specified, for example, as g.setLineDashes(10,2,2,2). The default dash pattern, of course, is a solid line with no dots or dashes.
The sample program StrokeDemo.java lets you draw lines and rectangles with a variety of line styles. See the source code for details.
13.2.2 Fancier Paints
So now we can draw fancier strokes. But all of our individual drawing operations have been restricted to drawing with a single color. We can get around that restriction by using Paint. An object of type Paint is used to assign color to each pixel that is "hit" by a drawing operation. Paint is an abstract class in package javafx.scene.paint. The Color class is just one concrete subclass of Paint. Any object of type Paint can be used as the parameter to g.setFill() and g.setStroke(). When a Color is used as the paint, it applies the same color to every pixel that is hit. However, there are other types of paint where the color that is applied to a pixel depends on the coordinates of that pixel. JavaFX has several classes that define paint with this property: ImagePattern and two kinds of gradient paint. In an image pattern, the pixel colors come from an image, which is repeated, if necessary, like a wallpaper pattern to cover the entire xy-plane. In a gradient, the color that is applied to pixels changes gradually from one color to another color as you move from point to point. Java has two gradient paint classes, LinearGradient and RadialGradient.
It will be helpful to look at some examples. The following illustration shows a polygon filled with two different paints. The polygon on the left uses a LinearGradient while the one on the right uses an ImagePattern. Note that in this picture, the paint is used only for filling the polygon. The outline of the polygon is drawn in a plain black color. However, Paint objects can be used for stroking shapes as well as for filling them. These pictures were made by the sample program PaintDemo.java. In that program, you can select among several different paints, and you can control certain properties of the paints.
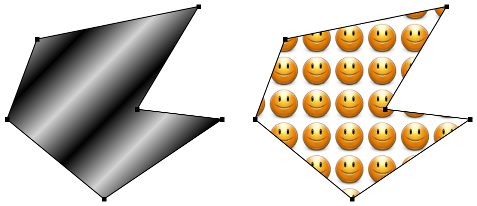
To create an ImagePattern, you first need an image. The Image class was introduced in Subsection 6.2.3. As we saw then, an Image object can easily be constructed from an image resource file, which is considered to be part of the program that uses it. Given an Image, pict, an ImagePattern can be created with a constructor of the form
patternPaint = new ImagePattern( pict, x, y, width, height, proportional );
The parameters x, y, width, and height are double values that specify the position and size of the image on the canvas. One copy of the image is placed with its top left corner at (x,y), and is scaled to the given width and height. The image is then repeated horizontally and vertically to fill the canvas (but you only see the part of the pattern that is within the shape to which the paint is applied).
The last parameter to the constructor is a boolean that specifies how x, y, width and height are interpreted. If proportional is false, the width and height are measured in the usual coordinate system on the canvas. If proportional is true, then width and height are measured in multiples of the size of the shape to which the paint is applied, and (x,y) is (0,0) at the upper left corner of the shape (more precisely, of the rectangle that just contains the shape). For example,
patternPaint = new ImagePattern( pict, 0, 0, 1, 1, true );
creates an image paint where one copy of the image just covers the shape. If the paint is applied to several shapes of different sizes, the paint will be scaled differently for each shape. If you want the shape to contain four copies of the shape horizontally and two copies vertically, you would use
patternPaint = new ImagePattern( pict, 0, 0, 0.25, 0.5, true );
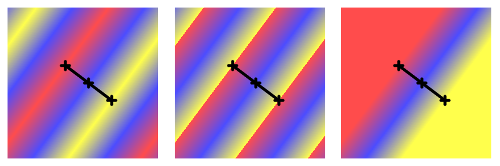
A linear gradient is defined by specifying a line segment and the color of several points along the line segment. The points and their associated colors are called color stops. Colors are interpolated between the color stops to give a color to each point on the line. The colors are then extended perpendicularly to the line segment to give an infinite colored strip. You also have to specify what happens outside that strip of color. In JavaFX, this is done by specifying a "cycle method." The possibilities are CycleMethod.REPEAT, meaning that the color strip is repeated to cover the entire plane; CycleMethod.MIRROR, meaning that the color strip is repeated, but every other copy is reversed so that the colors match up at the boundaries; and CycleMethod.NO_REPEAT, meaning that the color along each boundary is extended infinitely. Here are pictures of three red/blue/yellow gradients using the same original line segment and color stops. The picture on the left uses the MIRROR cycle method, the one in the middle uses REPEAT, and the one on the right uses NO_REPEAT. The basic line segments for the gradients are shown, and the positions of the three color stops on that line segment are marked:
The constructor for a linear gradient paint takes the form
linearGradient = new LinearGradient( x1,y1, x2,y2, proportional, cycleMethod,
stop1, stop2, . . . );
The first four parameters are double values that specify the endpoints of the line segment: (x1,y1) and (x2,y2). The fifth parameter, proportional, is a boolean; if false, the endpoints are specified in the usual coordinate system of the canvas; if true, they are specified in a coordinate system in which (0,0) is at the upper left corner of the shape to which the paint is applied, and (1,1) is at the lower right corner. The sixth parameter, cycleMethod, is one of the constants CycleMethod.REPEAT, CycleMethod.MIRROR, or CycleMethod.NO_REPEAT. The remaining parameters are the color stops for the gradient. A color stop is given as an object of type Stop. The constructor takes a double and a Color. The first parameter specifies the position of the stop along the basic line segment as a fraction of the distance from the first endpoint to the second endpoint. In general, the first color stop should have position 0, and the last one should have position 1, and the position value for each color stop should be greater than the position of the preceding color stop. As an example, the gradient paint for the first gradient in the above illustration was constructed as
grad = new LinearGradient( 120,120, 200,180, false, CycleMethod.MIRROR,
new Stop( 0, Color.color(1, 0.3, 0.3) ),
new Stop( 0.5, Color.color(0.3, 0.3, 1) ),
new Stop( 1, Color.color(1, 1, 0.3) ) );
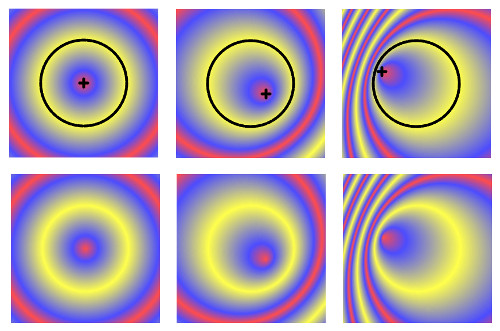
For a linear gradient, the color is constant along certain lines. For a radial gradient, color is constant along certain circles. For a basic radial gradient, color stops are specified along the radius of a circle, and color is constant along circles that have the same center as that circle. Colors outside the circle are determined based on the cycle method. Things are a little more complicated than that because a radial gradient can have a "focal point" inside the circle. For a basic radial gradient, the focal point is the center of the circle but the focal point can be any point inside the circle. The color of the gradient at the focal point is given by the color stop at position 0. The color along the circle is given by the color stop at position 1. It's easiest to see this in an illustration. The gradients in this picture are the same, except for the focal point. In the top row, the circle and the focal point are marked. Note that in all cases, the gradient is red at the focal point and yellow along the circle:
The constructor for a radial gradient has a lot of parameters...
radialGradient = new RadialGradient( focalAngle,focalDistance,
centerX,centerY,radius,
proportional, cycleMethod,
stop1, stop2, . . . );
The first two parameters specify the location of the focus. The focal distance is the distance of the focus from the center of the circle, given as a fraction of the radius; it must be strictly less than 1. The focal angle is the direction in which the focus is moved away from the center. For a basic radial gradient, the focal distance is 0, and the focal angle is irrelevant. The next three parameters specify the center and radius of the circle, and the remaining parameters are similar to the same parameters for linear gradients.
13.2.3 Transforms
In the standard drawing coordinates on a canvas, the upper left corner of the component has coordinates (0,0), and the coordinates (x,y) refer to the point that is x pixels over from the left edge of the component and y pixels down from the top. However, you are not restricted to using these coordinates. In fact, you can set up a graphics context to use other coordinate systems, with different units of length and different coordinate axes. You can use this capability to select the coordinate system that is most appropriate for the things that you want to draw. For example, if you are drawing architectural blueprints, you might use coordinates in which one unit represents an actual distance of one foot.
Changes to a coordinate system are referred to as transforms (or "transformations"). There are three basic types of transform. A translate transform changes the position of the origin, (0,0). A scale transform changes the scale, that is, the unit of distance. And a rotation transform applies a rotation about some point. Less common is a shear transform, which "tilts" an image. This illustration shows an original picture and several transformed copies of the picture:
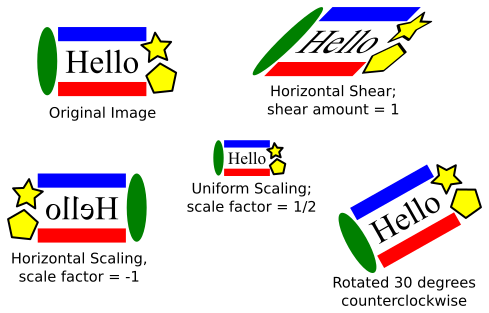
Notice that everything in the image, including the text, is affected by a transform.
You can make more complex transforms by combining transforms of the three basic types. For example, you can apply a rotation, followed by a scale, followed by a translation, followed by another rotation. When you apply several transforms in a row, their effects are cumulative. It takes a fair amount of study to fully understand complex transforms, and transforms are a major topic in a course in computer graphics. I will limit myself here to discussing a few simple cases, just to give you an idea of what transforms can do.
The current overall transform is a property of the graphics context. It is part of the state that is saved by the save() method and restored by the restore() method. It is especially important to use save() and restore() when working with transforms, to prevent the effect of a transform from carrying over from one subroutine call to another.
You should also remember that, like other properties of a graphics context, a transform affects things that are drawn after the transform is applied to the graphics context. It does not transform the picture that has already been drawn.
Suppose that g is of type GraphicsContext. A translation transform can be applied to g by calling g.translate(x,y), where x and y are of type double. Mathematically, the effect is to automatically add (x,y) to coordinates in subsequent drawing operations. For example, if you use coordinates (0,0) after applying the translation, you are actually referring to the point that had coordinates (x,y) in the usual coordinate system. All other coordinate pairs are moved by the same amount. For example the two statements
g.translate(x,y); g.strokeLine( 0, 0, 100, 200 );
draws the same line as the single statement
g.strokeLine( x, y, 100+x, 200+y );
In the second code segment, you are just doing the same translation "by hand." Instead of thinking in terms of coordinate systems, you might find it clearer to think of what happens to the objects that are drawn. After you say g.translate(x,y), any objects that you draw are displaced x units horizontally and y units vertically.
As an example, perhaps you would prefer to have (0,0) at the center of a component, instead of at its upper left corner. To do this, just use the following command before drawing anything:
g.translate( canvas.getWidth()/2, canvas.getHeight()/2 );
To apply a scale transform to g, use g.scale(sx,sy), where the parameters specify the scaling factor in the x-direction and the y-direction. After this command, x-coordinates are multiplied by sx, and y-coordinates are multiplied by sy. The effect of scaling is to make objects bigger or smaller. Scale factors greater than 1 will magnify sizes of shapes, while scale factors less than 1 will shrink the shapes. In many cases, the two scale factors are the same; this is called "uniform scaling."
The center of scaling is (0,0). That is, the point (0,0) is unaffected by the scaling, and other points move toward or away from (0,0). If an object is not located at (0,0), then the effect of scaling is not just to change its size but also to move it farther away from (0,0) (for scaling factors greater than 1) or closer to (0,0) (for scaling factors less than 1).
It is possible to use a negative scaling factor, which results in a reflection. For example, after calling g.scale(-1,1), objects will be reflected horizontally through the line x=0.
The third type of basic transform is rotation. The command g.rotate(r) rotates all subsequently drawn objects through an angle of r about the point (0,0). Angles are measured in degrees. Positive angles are clockwise rotations, while negative angles are counterclockwise (unless you have applied a negative scale factor, which reverses the direction of rotation).
Shearing is not considered a basic transform, since it can be done (with some difficulty) by a series of rotations and scalings. The effect of a horizontal shear is to shift horizontal lines to the left or right by an amount that is proportional to the distance from the x-axis. That is, the point (x,y) is transformed to (x+a*y,y), where a is the amount of shear. JavaFX does not have a method that applies a shear transform, but it does have a way to apply an arbitrary transform. For those who know some linear algebra, transforms are represented as matrices, and it is possible to specify a transform directly by giving the numbers that go in the matrix. A transform in JavaFX is represented by an object of type Affine, and the method g.transform(t) applies the Affine transform t to the graphics context. I don't want to go into the math here, but to do a horizontal shear with shear amount equal to a, you can use
g.transform( new Affine(1, a, 0, 0, 1, 0) );
Sometimes you will need to apply several transforms to get the effect you want. Suppose, for example, that you would like to show the string "hello world" tilted at a rising 30-degree angle and with its basepoint at (x,y). This won't do it:
g.rotate(-30);
g.fillText("hello world", x, y);
The problem is that the rotation applies to the point (x,y) as well as to the text. After the rotation, the basepoint is no longer at (x,y). What you need to do is make a rotated string with its basepoint at (0,0), and then translate by (x,y), which will move the basepoint from (0,0) to (x,y). That can be done as follows:
g.translate(x,y);
g.rotate(-30);
g.fillText("hello world", 0, 0);
The important thing to note is the order of the transforms. The translation applies to everything that comes after the translate command. What comes after it is some code that draws a rotated string with its basepoint at (0,0). That rotated string will be translated by (x,y). In effect, the string is first rotated, then translated. The rule for multiple transforms is that transforms are applied to objects in the opposite of the order in which the transform commands occur in the code.
The sample program TransformDemo.java can apply various transformations to a picture. The user controls the amount of scaling, horizontal shear, rotation and translation. Running the program might help you understand transforms, and you can read the source code to see how to code the transforms. Note that the transforms in this program are applied to the objects in the order scale-shear-rotate-translate. If you look in the code, you will see that the transform methods are called in the opposite order, translate-rotate-shear-scale. There is also an additional translation that moves the origin to the center of the canvas, so that the center of scaling, rotation, and shearing is at the center of the canvas.
13.2.4 Stacked Canvasses
The final example for this section is another simple paint program, ToolPaint.java. The paint programs in Chapter 6 could only draw curves. In the new program, the user can select a "tool" for drawing. In addition to a curve tool there are tools for drawing five kinds of shape: straight lines, rectangles, ovals, filled rectangles, and filled ovals.
When the user draws with one of the five shape tools, the user drags the mouse and a shape is drawn between the starting point of the drag gesture and the current position of the mouse. Each time the mouse moves, the previous shape is deleted and a new shape is drawn. The new shape doesn't actually become part of the picture until the user releases the mouse button. For the line tool, for example, the effect is that the user sees a line that stretches from the starting point to the current mouse position, and that line moves along with the mouse. I urge you to try the program to see the effect!
The difficulty for the programmer is that parts of the drawing are continually being covered and uncovered as the user moves the mouse around. When part of the current drawing is covered and then uncovered, the drawing must still be there! This means that while the user is dragging the mouse, the program can't simply draw the new shape on the same canvas that contains the current picture, since doing so would obliterate whatever was in that part of the picture.
The solution in JavaFX is to use two canvases, one stacked on top of the other. The bottom canvas contains the actual drawing. The top canvas is used to implement the shape tools. Ordinarily, the top canvas is completely transparent. That is, it is filled with a color that has alpha component zero. When a shape tool is being used, the shapes that are drawn as the user drags the mouse are drawn to the top canvas. The bottom canvas is not affected, but part of it is hidden behind the shape that was drawn in the top canvas. Each time the mouse moves, the top canvas is cleared, and a new shape is drawn to the top canvas. When the user releases the mouse at the end of the drag, the top canvas is cleared, and the shape is drawn to the bottom canvas, where it becomes part of the actual drawing. In the end, the top canvas is once again completely transparent, and the drawing in the bottom canvas is fully visible. Note that a canvas can be cleared to full transparency by calling
g.clearRect( 0, 0, canvas.getWidth(), canvas.getHeight() );
where g is a GraphicsContext for the canvas. (Canvasses are also fully transparent when they are first created.)
To stack one canvas on top of another, you can use a StackPane. A StackPane will simply stack up its child nodes one on top of the other, in the order in which they were added to the pane. The two canvasses in the program were set up like this:
canvas = new Canvas(width,height); // main drawing canvas canvasGraphics = canvas.getGraphicsContext2D(); canvasGraphics.setFill(backgroundColor); canvasGraphics.fillRect(0,0,width,height); overlay = new Canvas(width,height); // transparent top canvas overlayGraphics = overlay.getGraphicsContext2D(); overlay.setOnMousePressed( e -> mousePressed(e) ); overlay.setOnMouseDragged( e -> mouseDragged(e) ); overlay.setOnMouseReleased( e -> mouseReleased(e) ); StackPane canvasHolder = new StackPane(canvas,overlay);
Note that the mouse event handlers were added to the top canvas, since the top canvas covers the bottom canvas. When the user clicks on the drawing, it is actually the top canvas that is being clicked.
The curve tool, by the way, does not use the top canvas. Curves are drawn directly to the bottom canvas. Since no part of the curve will ever be deleted after it is drawn, there is no need to put a temporary copy in the top canvas.
13.2.5 Pixel Manipulation
ToolPaint.java has two more tools: "Erase" and "Smudge." (Both of these tools work directly on the bottom canvas.) The Erase tool does what it says: as the user drags the mouse, a small square around the mouse location is filled with the background color, erasing part of the drawing at that location. The Smudge tool is more interesting. Dragging with the smudge tool smears the color under the tool, as if you are dragging your finger through wet paint. In this picture from the program, the smudge tool was dragged around on the center of a red rectangle:

There is no built-in subroutine in JavaFX for smudging a picture. This is something that requires direct manipulation of the colors of individual pixels. Here is the basic idea: To implement the smudge tool, the program uses three 9-by-9 two-dimensional arrays of color components, one to hold the red components of the colors, one for the green components, and one for the blue. When the user presses the mouse while using the smudge tool, the color components of the pixels in a 9-by-9 square around the mouse location are copied into the arrays. When the mouse moves, some of the color from the arrays is blended into the colors of the image pixels at the new mouse location, and, at the same time, some of the color from the image is blended into the arrays. That is, the arrays drop off some of the color that they are carrying and pick up some of the color from the new location. (If you think about it, you should see that something similar happens when you smear paint with your finger.)
To implement this idea, we need to be able to read the colors of pixels in the image, and we need to be able to write new colors to those pixels. It is fairly easy to write colors to individual pixels, using something called a PixelWriter. If g is a GraphicsContext for a canvas, you can get a PixelWriter for the canvas by calling
PixelWriter pixWriter = g.getPixelWriter();
Then, to set the color of the pixel at (x,y) in the canvas, you can simply call
pixWriter.setColor( x, y, color );
where color is of type Color. (Note that x and y are pixel coordinates; they are not subject to any transform that might have been set in the graphics context.)
If JavaFX had a similarly easy way to read pixel colors from a canvas, we would be all set. Unfortunately, it is not so simple. The reason, as I understand it, is technical: It turns out that drawing operations do not immediately draw to the canvas. Instead, for efficiency, a bunch of drawing operations are saved and sent to the graphics hardware in a batch. Ordinarily, a batch is sent only when the canvas needs to be redrawn on the screen. This means that if you simply read a pixel color from the canvas, the value that you get would not necessarily reflect all of the drawing commands that you have applied to the canvas. In order to read pixel colors, you have to do something that will force all of the drawing operations to complete. The only way I know to do that is by taking a "snapshot" of the canvas.
You can actually take a snapshot of any scene graph node. A snapshot returns a WritableImage that contains a picture of the node, after all pending operations have been applied. It's easy to take a picture of an entire node:
WritableImage nodePic = node.snapshot(null,null);
The WritableImage will contain a picture of the node as it would appear on the screen, and it can be used in the same way as a regular Image object. The parameters are of type SnapshotParameters and WriteableImage. If a non-null writable image is provided, it will be used for the image, as long as it is large enough to contain a picture of the node; this can be more efficient than creating a new writable image. The SnapshotParameters can be used to get more control over the picture that is produced. In particular, they can be used to specify that the snapshot should contain only a certain rectangle within the node.
To implement the smudge tool, we need to grab the pixels from a small, 9-by-9 rectangle within the canvas. To do that efficiently, we can provide SnapshotParameters that pick out just that rectangle. We can then read the colors of the pixels using a PixelReader for the WritableImage. There are a lot of details, so I will just show you how it's done. In the program, I create a single WritableImage, a PixelReader, and a SnapshotParameters that will be used for all snapshots. Things are complicated a bit by the fact that some of the pixels in the snapshot might lie outside of the canvas, and I don't want to try to use color data for those non-existent pixels. Here is the code:
pixels = new WritableImage(9,9); // a 9-by-9 writable image pixelReader = pixels.getPixelReader(); // a PixelReader for the writable image snapshotParams = new SnapshotParameters();
When the uses presses the mouse, I need to take a snapshot of the 9-by-9 square in the canvas that surrounds the current mouse coordinates, (startX,startY). And I need to copy the color data from the snapshot into the color component arrays, smudgeRed, smudgeGreen, and smudgeBlue:
snapshotParams.setViewport( new Rectangle2D(startX - 4, startY - 4, 9, 9) );
// (The SnapshotParameter's "viewport" is the rectangle in the canvas
// that will be included in the snapshot.)
canvas.snapshot(snapshotParams, pixels);
int h = (int)canvas.getHeight();
int w = (int)canvas.getWidth();
for (int j = 0; j < 9; j++) { // row in the snapshot
int r = startY + j - 4; // the corresponding row in the canvas
for (int i = 0; i < 9; i++) { // column in the snapshot
int c = startX + i - 4; // the corresponding column in canvas
if (r < 0 || r >= h || c < 0 || c >= w) {
// The point (c,r) is outside the canvas.
// A -1 in the smudgeRed array indicates that the
// corresponding pixel was outside the canvas.
smudgeRed[j][i] = -1;
}
else {
Color color = pixelReader.getColor(i, j);
// pixelReader gets color from the snapshot
smudgeRed[j][i] = color.getRed();
smudgeGreen[j][i] = color.getGreen();
smudgeBlue[j][i] = color.getBlue();
}
}
}
To blend the color from the color component arrays into a square of pixels around another point (x,y), I need to take a new snapshot, this time of the 9-by-9 square of pixels surrounding (x,y). Once we have that snapshot, we can do the blending calculations and write the new color back to the canvas, using the PixelWriter that writes to the canvas:
snapshotParams.setViewport( new Rectangle2D(x - 4, y - 4, 9, 9) );
canvas.snapshot(snapshotParams, pixels);
for (int j = 0; j < 9; j++) { // row in the snapshot
int c = x - 4 + j; // corresponding row in the canvas
for (int i = 0; i < 9; i++) { // column in the snapshot
int r = y - 4 + i; // corresponding column in the canvas
if ( r >= 0 && r < h && c >= 0 && c < w && smudgeRed[i][j] != -1) {
// PixelReader gets current pixel color from the snapshot:
Color oldColor = pixelReader.getColor(j,i);
// Get a new color for the pixel by blending current color
// with the color components from the arrays:
double newRed = (oldColor.getRed()*0.8 + smudgeRed[i][j]*0.2);
double newGreen = (oldColor.getGreen()*0.8 + smudgeGreen[i][j]*0.2);
double newBlue = (oldColor.getBlue()*0.8 + smudgeBlue[i][j]*0.2);
// PixelWriter writes new pixel color to the canvas:
pixelWriter.setColor( c, r, Color.color(newRed,newGreen,newBlue) );
// Also blend some of the color from the canvas into the arrays:
smudgeRed[i][j] = oldColor.getRed()*0.2 + smudgeRed[i][j]*0.8;
smudgeGreen[i][j] = oldColor.getGreen()*0.2 + smudgeGreen[i][j]*0.8;
smudgeBlue[i][j] = oldColor.getBlue()*0.2 + smudgeBlue[i][j]*0.8;
}
}
}
This is a fairly complex operation, but I hope it gives you an idea of how to work with pixels. Remember that you can write pixel colors to a canvas using a PixelWriter, but to read pixels from the canvas, you need to take a Snapshot of the canvas, and use a PixelReader to read pixel colors from the WritableImage that contains the snapshot.
13.2.6 Image I/O
The sample paint program ToolPaint.java has a "File" menu with commands for loading an image from a file into the canvas and for saving the image from the canvas into a file.
To load the image from a file, you first need to load it into an object of type Image. We have seen in Subsection 6.2.3 how to load an Image from a resource file and how to draw that image onto a canvas. Loading the image from a file is not much different:
Image imageFromFile = new Image( fileURL );
The parameter is a string that specifies the file location as a URL—essentially a path to the file, preceded by "file:". If imageFile is an object of type File representing a path to the file, you can say
Image imageFromFile = new Image( "file:" + imageFile );
Typically, you would let the user select the file using a FileChooser dialog (Subsection 11.2.3), and imageFile would simply be the selected File returned by that dialog.
Of course, the user might select a file that can't be read or that does not contain an image. The Image constructor does not throw an exception in that case. Instead, it sets an error condition in the image object that you can check using the boolean-valued function imageFromFile.isError(). If an error did occur, you can get the exception that caused the error by calling imageFromFile.getException().
Once you have the image, and have checked that it was loaded without error, you can draw it to a canvas using a graphics context for the canvas. This command will scale the image to exactly fill the canvas:
g.drawImage( imageFromFile, 0, 0, canvas.getWidth(), canvas.getHeight() );
This is all put together in a method doOpenImage() that is used in ToolPaint to load an image from a user-selected file:
private void doOpenImage() {
FileChooser fileDialog = new FileChooser();
fileDialog.setInitialFileName("");
fileDialog.setInitialDirectory(
new File( System.getProperty("user.home") ) );
fileDialog.setTitle("Select Image File to Load");
File selectedFile = fileDialog.showOpenDialog(window);
if ( selectedFile == null )
return; // User did not select a file.
Image image = new Image("file:" + selectedFile);
if (image.isError()) {
Alert errorAlert = new Alert(Alert.AlertType.ERROR,
"Sorry, an error occurred while\ntrying to load the file:\n"
+ image.getException().getMessage());
errorAlert.showAndWait();
return;
}
canvasGraphics.drawImage(image,0,0,canvas.getWidth(),canvas.getHeight());
}
To save the image from a canvas into a file, you must first get the image from the canvas by making a snapshot of the entire canvas. That can be done with
Image image = canvas.snapshot(null,null);
Unfortunately, at least in the current version, it seems that JavaFX does not itself include any support for saving images to files. For that, it depends on something from the older "AWT" GUI toolkit: the BufferedImage class from package java.awt.image. A BufferedImage represents an image stored in the computer's memory, similar to an Image in JavaFX. A JavaFX Image can easily be converted into a BufferedImage, using a static method in class SwingFXUtils from package javafx.embed.swing:
BufferedImage bufferedImage = SwingFXUtils.fromFXImage(canvasImage,null);
The second parameter, which is null here, could be an existing BufferedImage to hold the image.
Once you have the BufferedImage, you can use a static method from class ImageIO, in package javax.imageio, to write it to a file:
ImageIO.write( bufferedImage, format, file );
The second parameter is a String that specifies the file format for the image. Images can be saved in several formats, including "PNG", "JPEG", and "GIF". ToolPaint always saves files in PNG format. The third parameter is of type File, and it specifies the file to be saved. ImageIO.write() will throw an exception if it is unable to save the file. (It can also fail without throwing an exception if it doesn't recognize the format.) Putting all this together gives the doSaveImage() method in ToolPaint:
private void doSaveImage() {
FileChooser fileDialog = new FileChooser();
fileDialog.setInitialFileName("imagefile.png");
fileDialog.setInitialDirectory(
new File( System.getProperty("user.home") ) );
fileDialog.setTitle("Select File to Save. Name MUST end with .png!");
File selectedFile = fileDialog.showSaveDialog(window);
if ( selectedFile == null )
return; // User did not select a file.
try {
Image canvasImage = canvas.snapshot(null,null);
BufferedImage image = SwingFXUtils.fromFXImage(canvasImage,null);
String filename = selectedFile.getName().toLowerCase();
if ( ! filename.endsWith(".png")) {
throw new Exception("The file name must end with \".png\".");
}
boolean hasFormat = ImageIO.write(image,"PNG",selectedFile);
if ( ! hasFormat ) { // (this should never happen)
throw new Exception( "PNG format not available.");
}
}
catch (Exception e) {
Alert errorAlert = new Alert(Alert.AlertType.ERROR,
"Sorry, an error occurred while\ntrying to save the image:\n"
+ e.getMessage());
errorAlert.showAndWait();
}
}