This is Quiz #2 from CPSC 100: Principles of Computer Science, Fall 1995. The answers given would receive full credit, but in many cases, there are variations or even completely different answers that would also receive full credit. The "Notes" are meant to clarify the answer or to provide some interesting extra information.
Question 1: The program you used in the lab, xLogicCircuits, allows you to "include" a previously saved circuit as a subcircuit inside another circuit that you are building. Explain why this ability is important, and explain what it has to do with structured complexity.
Answer: A circuit can be built directly out of AND, OR, and NOT gates--and in fact that's all that it is, really. But it would be difficult to design or understand a big, complicated circuit without organizing those gates into meaningful components. Otherwise, you just have a mass of meaningless detail. A subcircuit is a meaningful "chunk" of circuitry that can be used as a "black box" in constructing more complex circuits, which can then be used as subcircuits in even more complex circuits, and so on.
Note: Once again, I will note that a full answer to a question about structured complexity should show some awareness of the existence of hierarchical levels of complexity.
Question 2: What role is played by the ALU (arithmetic-logic unit) in a computer?
Answer: The ALU is the part of the CPU that does all the arithmetical and logical calculations that are required as part of executing a program. These operations include addition, shifting, multi-bit AND, etc.
Note: The ALU described in Chapter 2 of the text is simpler than the ALU's in real computers today. These might, for example, be able to do multiplication and division as well as addition and subtraction. But the basic idea is correct, and in fact early computers had ALUs that were even simpler. (Note that you shouldn't define an ALU as a "circuit with 7 control wires...", since that is something that won't be true for most ALUs. Also note that the "mini-ALU" from Lab #4 is much too simple to be useful in any real computer; it was meant as an exercise only.)
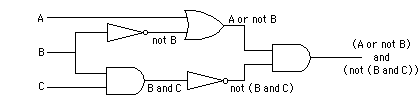
Question 3: Draw the logic circuit that corresponds to the Boolean algebra expression
(A OR NOT B) AND (NOT (B AND C))
Answer:

Question 4: Consider the following table, which specifies the output of a circuit for all possible combinations of two input values:
A B | OUTPUT
-------------|------------
OFF OFF | OFF
ON OFF | ON
OFF ON | ON
ON ON | OFF
Write down a Boolean algebra expression that expresses the value of Output in terms of A and B.
Answer: (A and (not B)) or ((not A) and B)
Note: Given a table of input/output values like this, there is a mechanical method for writing down a Boolean algebra expression that gives the specified output value for each combination of inputs. (See the text.) Once you have that expression, you can use it as a blueprint to build a circuit with the specified behavior. In general, although not in this particular case, that circuit will be more complicated than it has to be. But the important point is that it is always possible to build such a circuit in principle.
Question 5: Add the following two binary numbers:
1 1 0 1 0 0 1 1 1 0
1 1 1 0 0 0 1 0 1
----------------------
Answer: 10100010011
[by David Eck]