
| CPSC 120 | Principles of Computer Science | Fall 2024 |
The project is due at the time stated. No work will be accepted after 12/11 4:30pm except in the case of an incomplete. No late handins or extensions!
This course has introduced several core principles of computer science:
This course has also introduced several of the core constructs and concepts in programming:
Also central to computer science is the process of algorithm development — an algorithm is a series of steps built from those core constructs and concepts, and algorithm development involves being able to recognize when elements are applicable to the task at hand. We have focused specifically on when to use these elements in the context of interactive animated sketches, but the concepts — choosing between alternatives, repetition, and so on — are much more widely applicable.
And finally, we've also seen some of the things that programs can do, emphasizing topics in computer graphics and animation:
This project is a capstone project — the purpose is for you to demonstrate your mastery of the course material and to showcase what you can do. This project covers material from the whole course, but with an emphasis on the topics not covered in the midterm project (loops, arrays, fractals and self-similarity, behavioral animation, images and pixel-based manipulation).
As with the labs, you may get help with how to solve the problem and with writing and debugging code, but you must document any help received (including from TFs) and any resources used other than the textbook and posted course materials and you may not work together with other students to write code, shortcut to a solution by copying code or using someone else's program as a guide or example, or be in possession of someone else's program or solution before you have handed in your own.
Review the discussion in previous lab handouts and the full collaboration policy for more details.
To hand in your work:
Make sure that your name and a short description of the sketch are included in a comment at the beginning of your sketch.
Make sure that you've auto-formatted your sketch.
Copy the entire capstone directory from your sketchbook (~/cs120/sketchbook) to your handin directory (found inside /classes/cs120/handin).

Welcome to a (very fictional) North Dakota --
Blimps soar by, advertising the state. Crops grow by a lake surrounded by grass, with large mountains in the distance. An island with a magnificent tree floats back and forth across the lake. (It can also be positioned by holding the mouse button down and dragging.) A kite bobs in the wind. And a bald eagle (brown triangle with white head and tail, so clearly a bald eagle) soars overhead, causing the fish (which normally wander around trying not to run into each other) to scurry for cover and hide behind the island when they fall under its gaze (shown by the shaded rectangle).
(This is a screen shot rather than a running sketch because it runs too slowly in a web browser.)
Your task is to create a sketch named capstone which showcases what you've learned in this course. Since we've looked at several things related to modeling the natural world, some sort of landscape — like the fictional North Dakota — would be appropriate, but if you have other ideas, go for it! (Be creative!) Just make sure your sketch satisfies the requirements below.
For full credit your sketch must meet the following requirements.
In order to receive full points for an element, it must be both used appropriately and unique. "Used appropriately" means that the construct and pattern is appropriate for the situation — you can't just throw in a pointless 'if' statement or loop or use arrays when arrays are not needed in order to meet a requirement. It also means following the conventions for how things are to be used e.g. each function should have a single purpose (for example, a drawing function shouldn't also update animation variables) and the only variables that a drawing or filter function should access are that function's own parameters. "Unique" means that it is something new for this project, not simply copied over from a class example or the textbook or another assignment or very similar to a class or textbook example or something from another assignment. (Using elements directly from or substantially similar to examples or solutions in the textbook or from class or from your own sketches in previous labs or projects is acceptable with attribution — include a comment in your sketch identifying where the code came from — but won't count towards meeting the requirements of this assignment.)
Unless otherwise noted below, one element can satisfy more than one requirement e.g. an array of boids can address both "a bunch of things animated in a similar way using arrays" and "at least one thing or a group of things which use behavioral animation".
| category | requirements |
|---|---|
| representation, abstraction, and modularity |
Include:
|
| drawing, interaction, and animation |
Include:
|
| programming constructs |
Include:
|
| special topics |
Include four of the following:
|
| programming and software practice |
|
You can earn extra credit by going substantially beyond the required elements. There are too many possibilities to list, but here are a few specific elements as well as some more general ones:
Make me say wow! — add complexity (lots of shapes, elaborate patterns, more sophisticated motion paths, more complex behaviors or combinations of behaviors, etc), include all six of the special topics elements, have a particularly neat theme, or demonstrate exceptional creativity by combining the elements covered in new and interesting ways. If you've done something you think qualifies, point out what it is in a comment.
Include something that goes beyond what we've covered in the course — research a different L-system description or image filter or technique for generating fractals (such as iterated function systems and the Barnsley fern) or behavior or read about something new in the book. Note that this is not about copying code for something interesting from somewhere — you need to understand the idea and write your own code, not just copy someone else's code. Include a description of what the thing is and provide reference(s) to where you found the information about it.
Speed up the sketch by moving expensive-to-compute background elements (i.e. those involving recursion) to setup(): draw the non-animated background elements, copy the screen pixels into an image, and then, in draw() draw that image plus any animated or interactive bits.
Extra credit options for previous labs and projects can also provide some ideas. More creative and challenging elements will earn more points.
Plan first! Read carefully through the requirements and look through the rest of this section (especially the fractal clouds) so you know what that entails. Then come up with a topic or theme for your sketch and think about how you are going to incorporate all of the "include" requirements. Write your plan down in comments in your sketch — now you have a to-do list where you can cross off (delete) elements when you complete them.
Once you have a plan, start writing code. Utilize incremental development — add one thing at a time.
With lots of stuff (especially recursion), your sketch may run very slowly. If this happens, limit the depth of the recursion (don't use too large of a max depth for your plants, and don't let "too small" be too small for the fractal clouds — it's OK if they look a bit chunky) and the number of recursive elements (e.g. one plant instead of 20).
If you still want to be extravagant with recursion, see the extra credit options for a suggestion for speeding things up.
If you are including boids in your sketch, start with the template provided for lab 11 — copy the animation variables (declarations and initialization) and steps 1-4 in draw() into your sketch, array-ify those elements if your plans call for a large number of boids, and then focus on steps 2a and 2b.
You'll also need to add the boids library to your sketch — add a "boids" tab to your sketch and paste in the boids library code like you did in lab 11.
You can review the lab 11 handout for descriptions of many of the provided behaviors, but you'll also need to use at least one behavior that you didn't use in lab 11. The boids library file also contains behaviors that weren't described in the lab 11 handout — look through the file, focusing on the comments and the function headers, to find those behaviors and how to use them. (You can look at the bodies of the functions to see how the behaviors are implemented if you are curious, but it isn't necessary to do that to use them.)
You also need some way to keep your boids contained, either within a smaller region (as in the demo) or the window itself. Note that it is OK for the boids to leave the window or region temporarily, they just can't disappear offscreen indefinitely.
One option is to do this through behaviors, for example, if a boid leaves the window or region, it can switch to seek or a similar behavior to bring it back inside. (A containment behavior was discussed in class but isn't provided in the boids library — for a more math-intensive extra credit option, you could implement this behavior and use it.)
Alternatively, you can wrap the boid's position at the edge of the window or region (step 4b in the lab 11 template wraps at the edge of the window) or have the boids "bounce" — as with a bouncing ball, flip the sign of the x or y component of the boid's velocity when the boid hits the edge. (If you have problems with slow-moving boids escaping — much like slow-moving bouncing balls — see the "Physics Quirks" section in the midterm project.)

Fractal clouds can be generated using a midpoint displacement algorithm similar to what you used to generate the terrain in lab 7. Here's the idea:
| fractal terrain | fractal clouds | ||
|---|---|---|---|
 |
Start with a line segment connecting two points. (The y coordinates of the points can be equal, as shown in the example, or not.) |
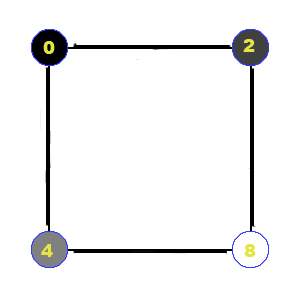 |
Start with a rectangle with a color associated with each corner. (the colors are 0, 2, 4, and 8 in this example) |
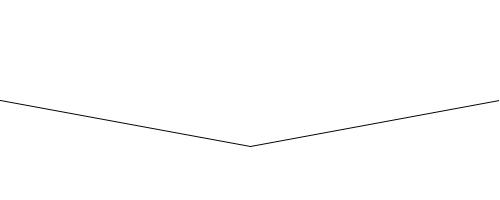 |
Replace each line segment with two new line segments which connect the original segment's endpoints with the "displaced midpoint". The displaced midpoint is the midpoint of the original segment, moved up or down by some amount — if the original segment's endpoints are (x1,y1) and (x2,y2), the displaced midpoint is ((x1+x2)/2,(y1+y2)/2+d) where d is a random amount. | 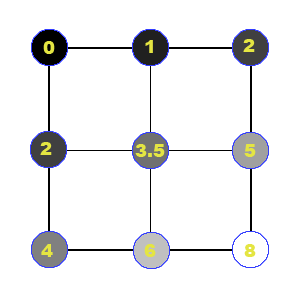 |
Replace each rectangle with four new rectangles as shown. The midpoint colors along each edge are the average of the colors of the adjacent corners (e.g. the top edge's color midpoint is (0+2)/2 = 1). The center color is the average of the four corner colors plus a random displacement (e.g. (0+2+4+8)/4 = 4.67 plus a random displacement = 3.5 as shown) |
   |
Repeat: replace each line segment with two line segments connecting each segment's original endpoints with a displaced midpoint. Keep going until the line segments are sufficiently short. At that point, draw the line segment. | 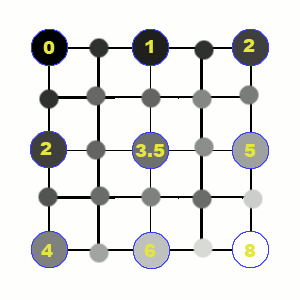
|
Repeat: replace each rectangle with four smaller rectangles with colors as shown. Keep going until the rectangles are sufficiently small. At that point, draw the rectangle using the average of its corner colors as its color. |
Observe that this process follows the replacement pattern — the rectangle in each level is replaced by four smaller rectangles, and only the final rectangle is actually drawn. The elements of the pattern:
The whole design is clouds — name your function drawClouds.
What changes from one level to the next are the position and size of the current rectangle, its four corner colors, and the maximum possible displacement maxd for the center color — this should decrease with each level to keep the color changes from becoming too abrupt. (As the rectangles get smaller, the displacement needs to get smaller so the color differences don't become too great.) All of these things (position, size, corner colors, and maximum displacement) will be parameters to the drawClouds function.
"Small enough" is based on the size (width and height) of the rectangle.
The base shape is a rectangle with the specified position and size, and whose color is the average of the corner colors.
There are four smaller copies with half the size (width and height) and position and corner colors as shown above and a maximum displacement half as big (maxd/2).
This description of the algorithm is meant to parallel the description of the fractal terrain from lab 7, and you can use your terrain function as an example of the structure though the details will be different.
Implementation notes:
For a blue sky with white clouds, you can get away with a single value for each corner's color so only four parameters are needed (one for each corner) rather than twelve (red, green, and blue for each corner). When you draw the rectangle, use fill(c,c,255) where c is the average of the corner color values. If you are drawing something other than clouds, you may need to have three color parameters for each corner. In that case, repeat the math done for the single color values for each of the red, green, and blue components.
Use the Processing function random to generate a random value between -maxd and maxd (the current maximum displacement) for d (the displacement added to the average of the corner colors to get the center color). Create a local variable for d since you will need to use the same value for each of the four smaller copies.
Experiment to find a good starting value for the max displacement — larger values will allow for greater contrast in the result. (However, a value bigger than 255 is not meaningful because color values are 0-255.)
Consider a rectangle to be small if both its height and width are small. Ideally "small" is just a few pixels, but if your sketch runs too slowly, make "small" larger — even large enough that you see a noticeable chunkiness in the pattern.
Since each frame involves generating the pattern from scratch, the random number sequence used for the displacements needs to be reproducible. Use randomSeed at the beginning of draw() so you don't get jumpy sky.