Homework 11
due Mon 2/26 in class

In all cases, start from vertex A unless otherwise indicated and break ties by considering vertices in alphabetical order. All three questions use the graph shown.

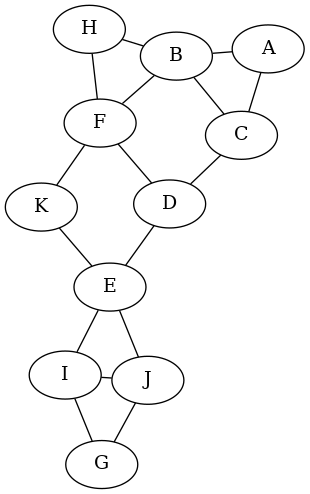
1. Find the unweighted shortest path from A to all other vertices for the graph shown. Show your work tracing the unweighted shortest path algorithm — show the contents of the queue at each iteration, indicate the order in which vertices are removed from the queue, and show a table of the dist labels as they are updated in each iteration of the while loop. (Have a column of the table for each vertex and a row for each iteration.)

2. Is the graph shown bipartite? If so, give a coloring; if not, explain why not. Show your work tracing breadth-first search until either the graph is colored or it is determined not to be bipartite — show the contents of the queue at each iteration, indicate the order in which vertices are removed from the queue, and show a table of the color labels as they are assigned in each iteration of the while loop. (Have a column of the table for each vertex and a row for each iteration.)

3. Carry out depth-first search on the graph shown, starting from vertex A. Indicate the order in which vertices are marked as "discovered" and as "processed". It can be beneficial if you make a mistake to show some additional evidence of your tracing, such as by showing a tree of the recursive calls.