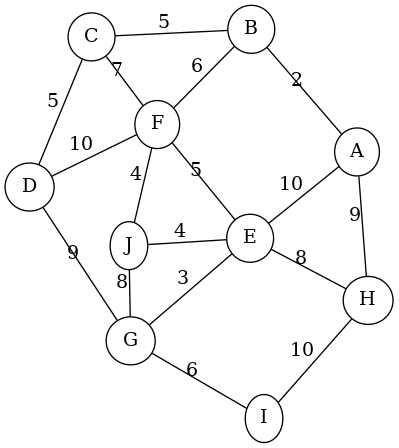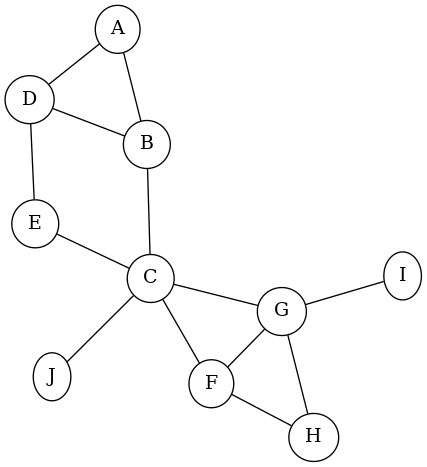
Find the cut vertices in the graph shown to the right.
Start the DFS from A, and show your work tracing the algorithm by identifying the tree and back edges in the DFS tree and by giving the entry labels and earliest reachable ancestor for each vertex. When there is a choice of what vertex to consider next, use alphabetical order.
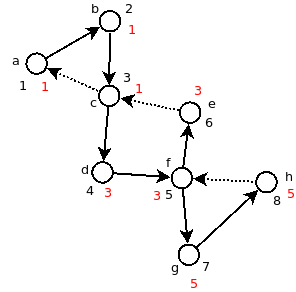
The example below illustrates a convenient way of showing your work. The entry times are shown in black and the earliest reachable ancestors in red in order to distinguish them. An alternative is to list entry times and earliest reachable ancestors in a table.
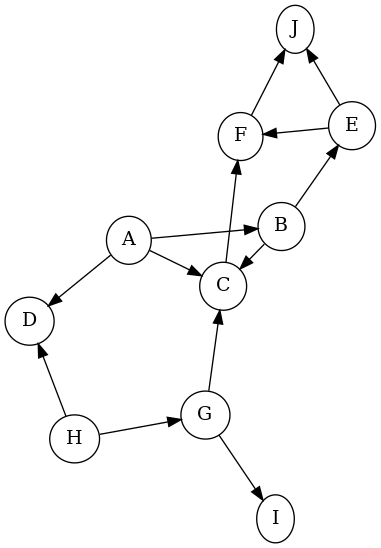
Perform a topological sort on the graph shown to the right, giving the resulting order of vertices.
Show your work tracing the algorithm by giving the exit labels computed for each vertex. When there is a choice of what vertex to consider next, use alphabetical order.
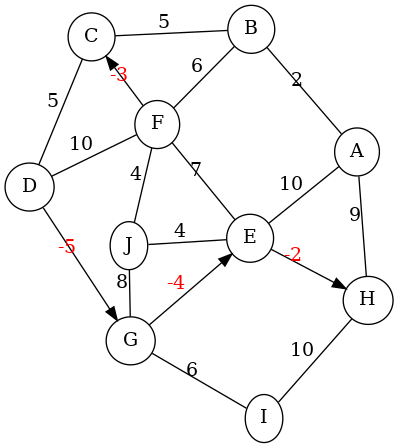
[corrected!] Carry out the Bellman-Ford algorithm on the graph shown to the right. (Negative weights are shown in red to make them easier to identify.) For clarity, when there are edges (u,v) and (v,u) with the same weight, a single undirected edge is shown.
Go through the edges in alphabetical order. (Be sure to consider both directions --- such as AB and BA --- for the undirected edges.)
Show your work tracing the algorithm by giving a table of the dist labels as they are updated in each iteration of the repeat loop. (Have a column of the table for each vertex and a row for each iteration.)