| CPSC 327 | Data Structures and Algorithms | Spring 2024 |
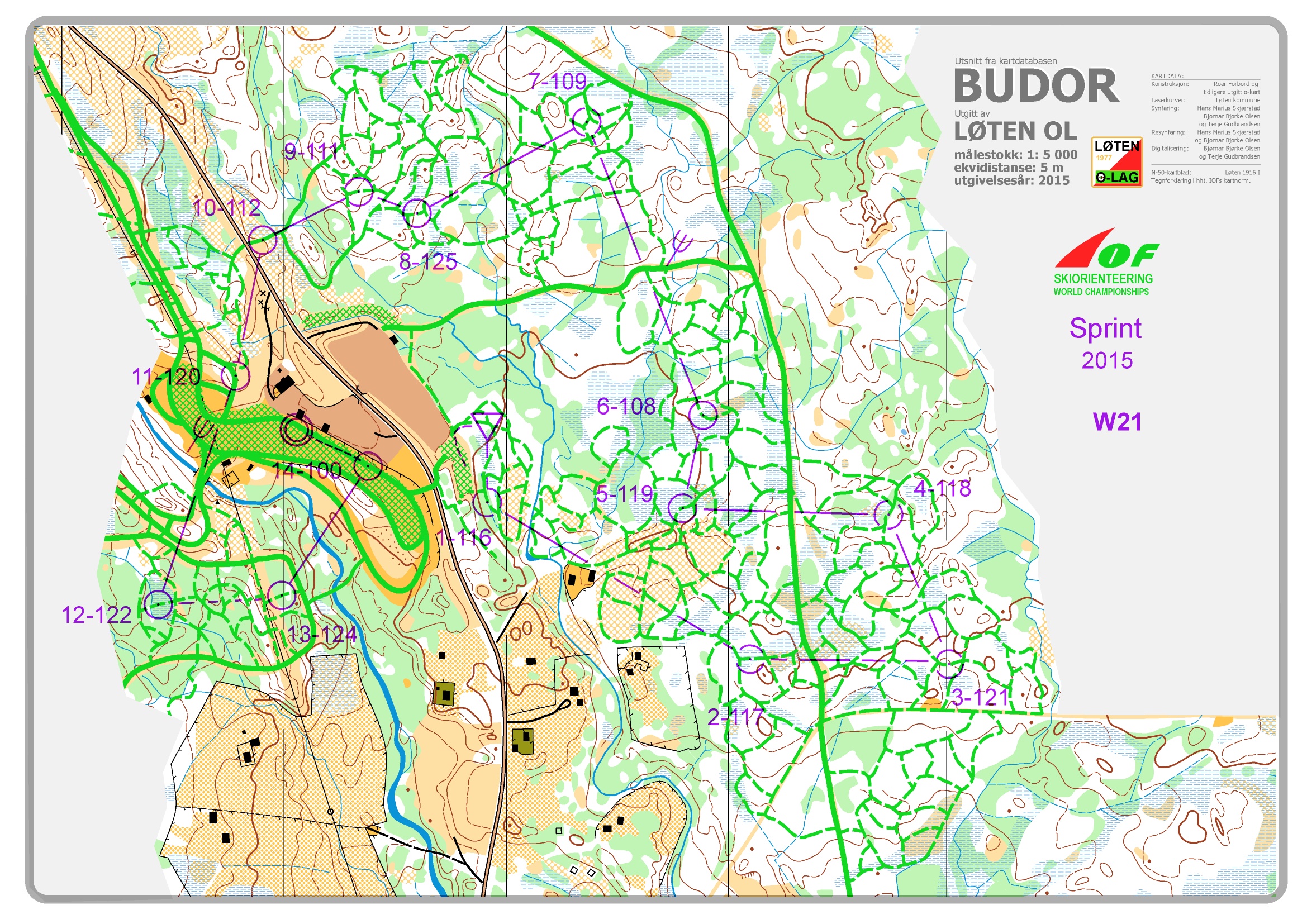

Ski orienteering is the sport of cross-country navigation on skis - competitors must navigate to a series of checkpoints (called controls) using a map and compass. An orange-and-white flag marks the location in the terrain. Controls typically must be visited in a particular order, and the goal is to navigate to a certain sequence of controls as quickly as possible.
Maps for ski-o (click for a larger version) show the track network, terrain, vegetation, and the course:
Tracks are shown with green lines. The symbol indicates the size of the trail — dashed lines are the narrowest and typically slowest, thick solid lines are the widest and typically fastest.
Contour lines are in brown.
Vegetation is shown with shades of yellow and green.
The course is in purple — a triangle for the start, circles for the controls, and a double circle for the finish. Straight lines between control circles and the first part of the number labelling each circle indicate the order in which the controls must be visited. (The second part of the number is the control code, which lets you verify that the flag you've found is the correct one.) Dashed purple lines indicate a marked (and mandatory) route.
It is OK to visit a control more than once (or visit controls not on your course) as long as there is a subsequence of controls visited that contains the right controls in the right order.
Model a ski-o race as a graph problem and give an efficient algorithm for finding the fastest route through the course.
Use the "design graphs, not algorithms" philosophy - design a graph so that the desired solution can be obtained from a standard graph algorithm (or algorithms) discussed in class, rather than customizing an algorithm or even designing one from scratch.
Be sure to fully describe how the graph is formulated - what do the vertices of the graph represent? The edges? Is the graph undirected or directed? Weighted or unweighted? (If weighted, what do the weights represent?) What is a solution to the problem in terms of the graph? Also address: Is the graph simple or not simple? Sparse or dense? Cyclic or acyclic? Provide a brief explanation with each answer.
You can make the following assumptions for this problem:
The start and finish are at track junctions.
All other controls are along tracks rather than at track junctions. They can be treated as being in the middle of the track segment (halfway between junctions).
It is possible to change directions at controls and return the way you came without continuing on to the next junction. It is not possible to change direction in the middle of any other track segment.
No shortcuts — you must stay on a track and not cut between tracks. (This is not the case in actual competition.)
There aren't any mandatory routes that must be followed.
There are no one-way trails, but note that the speed of travel in one direction may be very different from the other direction. (e.g. going in the uphill direction vs the downhill direction)