| CPSC 327 | Data Structures and Algorithms | Spring 2024 |
Using the code provided in /classes/cs327/dijkstra/, implement Dijkstra's algorithm as discussed below.
Dijkstra's algorithm is a graph algorithm, and is most efficient with an adjacency list implementation of the Graph ADT. You can either use your own implementation (if you implemented AdjacencyListGraph in programming assignment 1) or the provided implementation in graph.jar. To use the jar file, import it into your Eclipse project, right-click on it in the Package Explorer, and choose Build Path -> Add to Build Path.
Implement Dijkstra's algorithm as discussed in class (with the modification noted below) in Dijkstra.java — replace the method and constructor bodies that throw an UnsupportedOperationException with code that works as described in the method and constructor comments. (Note that init(s) and run(f) together cover Dijkstra's algorithm — init initializes the dist and prev labels and the priority queue, and run carries out the main loop.) The modification is to change prev so that prev[u] = e — store the edge along which a shorter path to u was discovered rather than the vertex v from which the shorter path to u was discovered. This makes it easier to implement getPathEdges.
Assume that the edge weights are double values, but do not make any assumptions about how the edge weights are stored in the graph. That's the reason for the EdgeWeight parameter to the constructor — EdgeWeight has a method weight(Edge), so w.weight(e) returns the weight for edge e.
Use Java's PriorityQueue for the priority queue. Two notes —
PriorityQueue requires either that the elements in the queue are Comparable or that a Comparator is defined. Since there isn't really a natural ordering for Vertex (there are many ways one might choose to order vertices), the latter option should be used. The provided code includes an inner class VertComparator for this purpose — implement the compare method so that it returns -1, 0, or 1 depending on whether vertex u should come before vertex v, is tied with vertex v, or should come after vertex v in the priority queue's ordering. (Recall that the priority queue is ordered by the vertex's dist label, and also know that Java's scoping rules mean that instance variables in the parent class are visible in the inner class, even if private.) Provide an instance of the comparator to PriorityQueue's constructor; see the API.
PriorityQueue does not have a decreaseKey operation. It is OK to remove and re-add the vertex instead, even though the remove operation is O(n).
run(f) only needs to find the shortest path to vertex f, so it should break out of the loop after vertex f is removed from the priority queue. (f == null meeans that the shortest paths to all vertices should be found so the loop runs until the priority queue is empty — do this case need special handling?)
getPathVertices(f), getPathEdges(f), and getDist(f) return information about the shortest path to vertex f. getDist should return the dist label assigned to f. getPathVertices and getPathEdges should return the vertices and the edges, respectively, on the shortest path from s to f (including s and f). They return an Iterable; the simplest solution here is to create and return an instance of some already-existing collection that implements Iterable, such as a List of some kind (e.g. ArrayList or LinkedList).
You do not need to check the "requires init(s) [or run(f)] to have been called first" preconditions.
Other than the exception for decreaseKey, your implementation should match the running time discussed in class. In particular, make sure that getPathVertices and getPathEdges are O(1) per element, that is, O(n) and O(m), respectively.
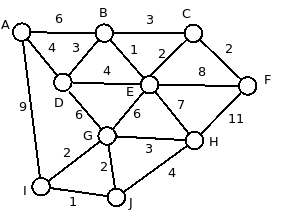
The main program Main.java provides a test case --- it creates the graph shown, runs Dijkstra's algorithm to find the shortest paths from A to all other vertices, and prints out those paths and their lengths. Use it to test your implementation, and feel free to modify it however you want for further testing purposes.
The output of the provided main program should be:
A -> J: 10.0 path vertices: A I J path edges: AI/9 IJ/1 A -> I: 9.0 path vertices: A I path edges: AI/9 A -> H: 13.0 path vertices: A D G H path edges: AD/4 DG/6 GH/3 A -> G: 10.0 path vertices: A D G path edges: AD/4 DG/6 A -> F: 11.0 path vertices: A B C F path edges: AB/6 BC/3 CF/2 A -> E: 7.0 path vertices: A B E path edges: AB/6 BE/1 A -> D: 4.0 path vertices: A D path edges: AD/4 A -> C: 9.0 path vertices: A B C path edges: AB/6 BC/3 A -> B: 6.0 path vertices: A B path edges: AB/6 A -> A: 0.0 path vertices: A path edges:
The Graph ADT only addresses the graph structure — it does not require elements like edge weights, nor does it prescribe how such additional information should be stored. In order to make the implementation of a graph algorithm like Dijkstra's algorithm as flexible as possible, it should similarly not make assumptions about how edge weights are stored. Instead, a "get weight" function that can be used when edge weights are desired is passed to the constructor — or, since Java doesn't truly support first-class functions, an object with a "get weight" function is passed to the constructor. (This is the same design principle behind the comparator object passed to PriorityQueue in order to allow different means of ordering the elements.)
"Object with a 'get weight' function" is implemented with the EdgeWeight interface in Dijkstra.java. The constructor's caller must then supply an instance of EdgeWeight. This can be done by defining a class that implements EdgeWeight and creating an instance of that class, but lambda expressions provide an alternative when the type is a functional interface (an interface containing a single subroutine). You can see the following in the provided Main:
Dijkstra alg = new Dijkstra(g, e -> ((Integer) e.getObject()).doubleValue());
You don't need to know about lambda expressions in order to implement the methods in Dijkstra, but you can read more about them here if you are curious what the code above means.
Address the following:
Implementing decreaseKey by removing and re-inserting the element in the priority queue raises the running time of that operation to O(n). What does that mean for the overall running time of your implementation of Dijkstra's algorithm? Give the running time and explain where it comes from.
Removing from the priority queue is the expensive part. What if that step is skipped? That is, leave the vertex with the old distance in the priority queue and add just add another copy with the new distance. Consider what this means for the algorithm — is special handling needed when vertices are removed from the priority queue in order to accommodate duplicate vertices? Explain. Then, what does this strategy do to the running time of decreaseKey as well as the overall running time for Dijkstra's algorithm? Give the running times and explain where they come from.
Note: hand in the redo as dijkstra-redo rather than copying over the original handin.
Hand in your code by copying your Java files into a folder called dijkstra within your handin directory (/classes/cs327/handin/username).
Hand in a hard copy of your writeup for the extra credit.