CPSC 120, Spring 2002
Third Test, April 17
This is the third test from CPSC 120: Principles of Computer Science, Spring 2002.
Question 1: Computer graphics uses hierarchical models for building complex scenes from simple shapes. Explain what this means and why it is important, and explain how hierarchical models are constructed in xModels.
Answer: Complex graphics models are made from very simple geometric shapes such as circles and triangles. As usual, this complexity is manageable because it is structured complexity. Simple shapes can be combined to make more a more complicated object. That object can then be manipulated as a single thing. For example, geometric transformations can be applied to the object as a whole. Once objects have been defined in this way, they can be used to build even more complex objects, which can in turn be used as building blocks in the next level. (This is what it means to say that hierarchical models are used.) In xModels, it is the DEFINE command that makes it possible to define new objects from simpler parts.
Question 2: Discuss the use of activation records for implementing subroutines. What is an activation record? When are they created and destroyed? What information is stored in an activation record? How are they related to recursion?
Answer: When a subroutine is called, an activation record is created to hold all the information that is needed while the subroutine is running. This includes the values of the parameters and local variables of the subroutine. It also includes a return address, which records where in the program the subroutine was called. This allows the computer to return to what it was doing after it finishes executing the subroutine. When the subroutine ends, the activation record is destroyed, since the information that it contains is no longer needed. When one subroutine calls another, the activation record for the second subroutine is simply "stacked" on top of the activation record of the first. This is especially important for keeping track of recursion. When a subroutine calls itself, it will have several activation records on the stack at the same time.
Question 3: The task of writing programs can be made easier by paying attention to preconditions and postconditions. Define these terms and explain how they can be used to help develop programs. (An example would be useful.)
Answer: A precondition is something that must be true at a certain point in the program, if the program is to continue on from that point without error. For example, the statement "A := B/C" has the precondition that C is not zero, since if C is zero, a division-by-zero will occur. As another example, a recursive subroutine that begins
SUB recur(parm)
IF (parm > 0)
recur(parm - 1)
.
.
.
has the precondition that the parameter must not be less than zero, since if it is, an infinite recursion error will occur. As a final example, if you want to draw something in xTurtle, a precondition is that the pen must be down. On the other hand, a postcondition is something that is guaranteed to be true after some chunk of code is executed. For example, a postcondition of the command PenDown is that the pen is down. A postcondition of the loop
LOOP
AskUser("Enter a non-zero value for C", C)
EXIT IF C <> 0
END LOOP
is that the value of C is not zero. Paying attention to preconditions and postconditions can be helpful when developing programs. The key is to look for preconditions. When you notice that a precondition is required at some point in the program, you know that you have to either check that it holds or insert code to make it hold. That is, the precondition of a chunk of code should be a postcondition of the code that precedes it in the program.
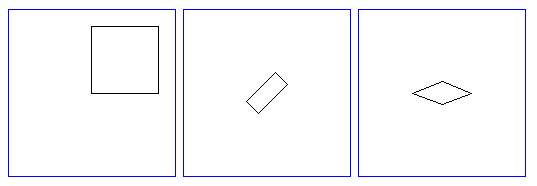
Question 4: Show the picture that would be produced by each of the following short xModels programs:
a) square scale 8 translate 4,4
b) square scale 5,2 rotate 45
c) square rotate 45 scale 5,2
Answer: In part a), an 8-by-8 square is moved over 4 units and up 4 units, putting its center at (4,4) and its lower left corner at (0,0). In part b), a 5-by-2 rectangle is rotated 45 degrees about its center. In part c), a square is first rotated 45 degrees, giving something that looks more like a diamond. This diamond is then stretched out by a factor of 5 in the horizontal direction and by a factor of 2 in the vertical direction, giving a diamond shape that is wider than it is tall. Here are pictures, as produced by xModels:
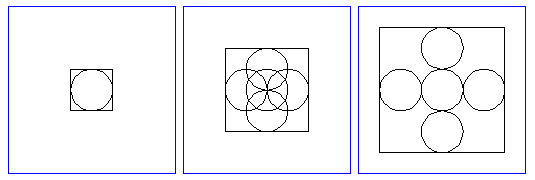
Question 5: Describe the animation produced by the following xModels program. Draw a few frames from the animation to illustrate your answer. (Suggestion: Start by drawing the first frame and the last frame.)
animate 30
circle scale 5
circle scale 5 translate 0, 0:5
circle scale 5 translate 0, 0:-5
circle scale 5 translate 0:5, 0
circle scale 5 translate 0:-5, 0
square scale 5:15
Answer: Initially, there are five circles that all all on top of each other so it looks like one circle (since in the first frame all the translations are 0,0). Then, four circles start spreading out. One moves up, one moves down, one moves left, and one moves right. One circle remains stationary. At the end of the animation, each moving circle has moved 5 units, which is the same as its diameter. Also in the picture is a square, which grows from 5 units to 15 units wide. This square always exactly enclosed the circles. The moving circles are always tangent to the sides of the square. Here are the first, middle, and last frames from xModels:
Question 6: There are two types of parameters, dummy parameters and actual parameters. Explain these terms, and give an example.
Answer: Dummy parameters are used in subroutine definitions to represent values that will be passed to the subroutine when it is called. Actual parameters are the values that are passed when the subroutine is called. The actual parameter values are assigned to the dummy parameters before the body of the subroutine is executed. For example, in a subroutine definition of the form
SUB drawit(length,count)
.
.
.
END SUB
the dummy parameters are length and count. If this subroutine is used in the subroutine call statements drawit(5,10) and drawit(x,num+5), for example, then the 5, 10, x, and num+5 are all actual parameters.
Question 7: Write an xTurtle subroutine named rect that can be used to draw rectangles. The width and the height of the rectangle should be given as parameters. For example, the command rect(5,2) will draw a rectangle that is five units long and two units high. At the end of the subroutine, the turtle should be in the same position and facing the same direction as it was at the beginning.
Answer: There are many ways to do this. Here are two. The first (and most likely) draws the rectangle so that its lower left corner is at the turtle position. For the second, the turtle is in the middle of the top side of the rectangle:
SUB rect(length,width) SUB rect(length,width)
forward(length) forward(length/2)
turn(90) turn(-90)
forward(width) forward(width)
turn(90) turn(-90)
forward(length) forward(length)
turn(90) turn(-90)
forward(width) forward(width)
turn(90) turn(-90)
END SUB forward(length/2)
END SUB
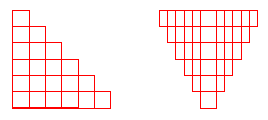
Question 8: Assume that rect is the subroutine from the previous problem. Draw the picture that will be produced by the following loop:
DECLARE L, W
L := 6
W := 1
LOOP
rect(L,W)
L := L - 1
W := W + 1
EXIT IF L = 0
END LOOP
Answer: The exact picture will depend on the answer to Question 7. Here are pictures drawn by the two subroutines given above:
Question 9: Explain how HTML and PHP can be used together to write interactive Web pages. (This is a 13-point essay question. Please give a reasonably detailed answer.)
Answer: HTML is a language that is used to write Web pages. For interactivity, a Web page can include HTML "forms" where the user can enter data. This data is sent back to the Web server to be processed. The Web server then creates a new HTML page that is sent back to the Web browser to be viewed by the user. One way for this to be handled is with a PHP program. PHP is a programming language that can be used to write programs that will run on a Web server. The program can be run by the server to process data from a form. The output of the program is the HTML code that is sent back to the user as a response. PHP is very convenient for this purpose because of the way that the form data is given to the program. Each piece of data in the form has a name. This name simply becomes a variable in the PHP program whose value is the data entered by the user. Then the PHP program can simply use the data to create its output.
Question 10: Consider the following recursive xTurtle subroutine:
SUB guess( length, complexity )
DECLARE count
count := 0
turn( 45 )
LOOP
forward( length )
IF ( complexity > 1 ) THEN
guess( length / 3, complexity - 1 )
END IF
back( length )
turn( 90 )
count := count + 1
EXIT IF count = 4
END LOOP
turn( -45 )
END SUB
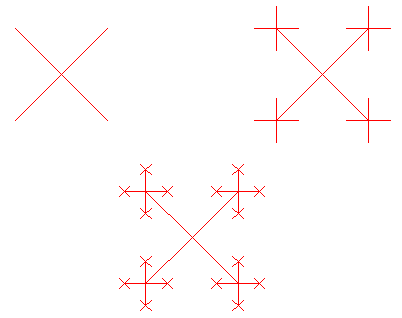
In parts a), b), and c), show the picture that is produced by the subroutine call:
a) guess(9,1)
b) guess(9,2)
c) guess(9,3)
For extra credit: Find a formula that can be used to compute the
number of lines drawn (that is, the number of times that the
"forward" command is called) when guess(9,N) is executed, for
any given value of N. Explain why your answer is valid.
Answer: For part a), four lines are drawn radiating out from the center at intervals of 90 degrees. Because of the turn(45), the first line is at 45 degrees, and the picture looks like an X. For part b), the same lines are drawn, but a smaller-sized copy of the first picture is drawn at the tip of each line. The copies are also rotated by 45 degrees, which makes the lines in the copies horizontal and vertical. In part c), a large X is drawn, with reduced copies of the previous picture at the tip of each line. Here are the pictures produced by xTurtle:
For the extra credit problem, if the complexity is N, then the number of lines is 4 + 42 + 43 + ... + 4N. In the move from complexity A to complexity A+1, four lines are added onto the tip of each line. There are 4 lines in the first picture. In the second picture, 4 new lines are added at the tip of each of 4 lines for a total of 42 new lines. In the third picture, 4 new lines are added at the tip of each of 42 lines for a total of 43 new lines.... In the Nth picture, 4N new lines are added. If we add up all the new lines on each level, the total is 4 + 42 + 43 + ... + 4N.