In this lab, you will be working with recursion. In the first part of the lab, you will write a program that generates random sentences based on a set of syntax rules. In the second, you will use recursion to create pictures of fractals.
You can start the lab by creating an Eclipse project named "lab3." Add the files Fractals.java and SimpleRandomSentences.java, from the directory /classes/s10/cs225 to your Eclipse project.
This lab will be due on Thursday of next week, at the beginning of Lab 4. By that itme, ou should copy your project from your Eclipse workspace into your homework folder in /classes/s10/cs225/homework.
The grammar of natural languages such as English exhibits a recursive structure. This structure can be expressed in syntax rules written in the format known as BNF (Bachus-Naur Form, named after the people who invented it). You have proably seen BNF used to specify the syntax of programming languages. While BNF is ordinarily used as a guide for parsing (that is, determining whether and how a given string follows the syntax rules), it can also be used a a guide for generating strings that follow the syntax rules. An example of this can be found in the sample program SimpleRandomSentences. In this example, each syntax rule -- except those that just give lists of possibilities -- is represented by a method in the program. The method for a rule generates strings that follow that rule. Where one syntax rule refers to another rule, the method that represents the first rule calls the method that represents the second rule. (You should run the program to see what it does, and you should read the code and try to understand it.)
For the first exercise of the lab, you should write a similar program that implements the following rules to generate random sentences:
<sentence> ::= <simple_sentence> [ <conjunction> <sentence> ]
<simple_sentence> ::= <noun_phrase> <verb_phrase>
<noun_phrase> ::= <proper_noun> |
<determiner> [ <adjective> ]... <common_noun> [ who <verb_phrase> ]
<verb_phrase> ::= <intransitive_verb> |
<transitive_verb> <noun_phrase> |
is <adjective> |
believes that <simple_sentence>
<conjunction> ::= and | or | but | because
<proper_noun> ::= Fred | Jane | Richard Nixon | Miss America
<common_noun> ::= man | woman | fish | elephant | unicorn
<determiner> ::= a | the | every | some
<adjective> ::= big | tiny | pretty | bald
<intransitive_verb> ::= runs | jumps | talks | sleeps
<transitive_verb> ::= loves | hates | sees | knows | looks for | finds
As in SimpleRandomSentences.java, you can use arrays to implement the last seven rules in this list. (You might improve on that program by writing a single method "void String randomItem(String[] listOfStrings)" for picking a random item from an array of strings.) You are welcome to add to or modify the items in the lists given here.
For each of the first four rules, you should write a method to represent that rule. Note that a choice of alternatives (represented in the rules by "|") can be implemented using a switch or if..else statement; the various choices don't necessarily have to have the same probability. An optional element (represented by brackets, "[ xxx ]") can be implemented by a simple if. And a repeated optional element (represented by brackets with dots, "[ xxx ]...") can be represented by a while loop. You should implement the first four rules exactly as stated here. The main routine should call the <sentence> method to generate random sentences. (You can use the main routine from SimpleRandomSentences.java if you want.
You have to be careful in this program to avoid infinite recursion. Since it will use random choices, there is no guarantee that the recursion will ever end. If your probabilities of doing recursion and continuing loops are too high, it is possible for the program to get lost in recursive calls forever -- or to produce some finite but ridiculously long sentences. You should adjust your probabilities to make sure that this doesn't happen, but that you still get some interesting sentences.
A "fractal" is a geometric figure that has some kind of "self-similarity." In one type of fractal, the self-similarity is an exact recursive structure: The figure is made up of several pieces that are scaled-down copies of itself. For a true fractal, the recursion is infinite; each scaled-down copy is itself made up of smaller copies, which are made up of even smaller copies, and so on forever. On the computer screen, we can get good approximations of fractals by limiting the recursion to a finite level.
In class, we discussed the Koch Curve, an infinitely convoluted path from a point A to a point B. For this second part of the lab, you will work with a program that can draw Koch Curves as well as some other fractals. The file Fractals1.java is a starting point for this exercise. It can already draw Koch Curves, and the user interface of the program is fully implemented. You just have to code the methods that draw the other two types of fractals, Sierpinski Triangles and Sierpinski Carpets. Here is an applet version of the completed program:
To complete Fractals1.java, you only have to fill in the code in the methods drawSierpinskiTriangle and drawSierpinskiCarpet. You should read the comments on those methods, and you should read and try to understand the code in the drawKochCurve method (even if you don't understand exactly how I picked the points in that case).
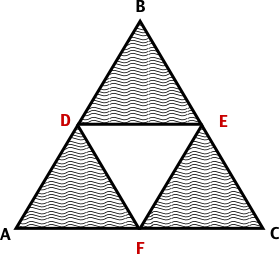
A Sierpinsky Triangle is a triangular fractal that is made up of three triangular parts that are simliar to the whole:

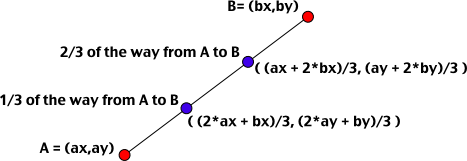
In the recursive case, you are given the vertices A, B, and C of a big triangle. To create the smaller triangles, you need to find the points D, E, and F, which are the midpoints of the sides of the big triangle. Given the coordinates of two points, it's easy to find the coordinates of the midpoints of the line between them:

The classic Sierpinski Carpet is a rectangular fractal made up of 8 rectanglular parts that are simlilar to the whole, arranged as shown in this picture:

In this case, given the four vertices of the big rectangle, you have to find the coordinates of the points that are 1/3 of the way and 2/3 of the way from one vertex to the next. Again, there are simple formulas for this:
The Sierpinsky Carpet idea can be generalized in a nice way. The big rectangle is divided into 9 sections. In the classic Carpet, 8 of those sections are included in the recursion, while the middle section is left out. This can be generalized by choosing a different set of sections to leave out. In the completed program, there is a set of 9 checkboxes that correspond to the 9 sections of the rectangle. Each checkbox controls whether or not the corresponding section of the rectangle is left out of the recursion. The settings of the 9 checkboxes show up in the method that you have to write as an array of boolean values. You should take these boolean values into account as you do the recursion.
Note that many different settings of the checkboxes give attractive and maybe surprising results. Try it!