CPSC 225, Spring 2011
Lab 3: Three Exercises in Recursion

For this lab, you will be working on three examples of recursion. In each case, much of the program is given to you, and you just have to complete it. For the first two exercises, you just have to fill in the inside of a recursive method. If you understand how the recursion works, those two exercises shouldn't take you too long. You will have to write more code for the third exercise.

Create a new Eclipse project. Open the directory /classes/s11/cs225/files-for-lab-3, and copy its contents into the src folder of your project. Two of the items in this directory are subdirectories: mines and resources. You can copy-and-paste a directory into your src folder in the same way that you copy-and-paste a file.

The lab is due at the beginning of next week's lab.

Exercise 1: Sierpinski Carpet

The first exercise is about fractals. A fractal is a geometric figure that exhibits "self-similarity." In a perfect fractal, the entire figure is made up of several smaller copies of the figure. The Sierpinski carpet is one famous example. A Sierpinski carpet is a square divided into nine subsquares. Eight of the subsquares -- all except for the middle one -- contain 1/3-sized copies of the entire figure.

Drawing perfect Sierpinski carpet would require infinite recursion, but we can draw an approximation of one using a finite level of recursion. The program SierpinskiCarpet.java will be able to do that -- as soon as you implement a recursive method to do the drawing. The program will also draw variations on the Sierpinski carpet in which the user selects which of the nine subsquares of the main square should contain copies of the fractal.

Open the file SierpinskiCarpet.java. The method that you have to complete is at the very end:

         private void drawCarpet(Graphics g, int level, int x, int y, int size)

As currently implemented, this method simply draws a filled sqaure with the specified size, with upper left corner at (x,y). It should be a recursive method, where the level parameter tells how many levels of recursion should be done. When the level is zero, it should simply fill in the square. When the level is greater than zero, it should divide the square into three rows and three columns, and it should call itself to draw a (level-1) figure in some of the subsquares. The subsquare in row r, column c is to be filled if the corresponding checkbox is checked, that is, if checks[r][c].isSelected() is true.

You do not have to do any work on this program outside the drawCarpet method. You can complete this method by adding somewhere between about six and twenty lines of code. Here's the completed program showing an approximate fractal in which five of the subsquares hold copies of the full fractal:

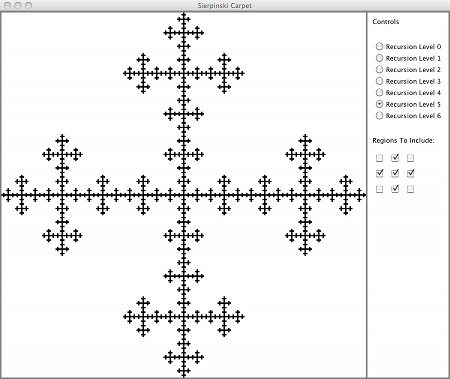
Exercise 2: Recursion in MineSweeper

MineSweeper is a game in which the user clicks squares that might or might not hold mines. If the user clicks a mine, the mine explodes and the game ends. If the user clicks a safe square, then the user is told how many neighboring squares contain mines. The number of mines is displayed in the square that was just clicked; if the number is zero, no number is displayed.

In my version of the game (based on an old Macintosh version), the goal is to reveal a safe path from the upper left square to the lower right square. The user can only click on squares that are next to squares that have already been revealed as safe. The user can right-click a square to indicate that the user believes that it contains a mine; right-clicking again on a marked square will unmark it.

The program is contained in the package named mines. The main program is in MineSweeper.java. You can run this program. The game is fully functional, but is annoying to play because of a lack of recursion! Your job is to add in the recursion and make the game more playable.

If you click a square where the number of mines in the neighboring squares is revealed to be zero, then you know that all the neighbors of that square are also safe. Since there is no thought involved in clicking on those squares, the computer should do it for you! Furthermore, if any of those square also have a bomb count of zero, all their neighbors should also be clicked. And so on. To do this out to any number of neighbors, you need recursion.

In the program, when the user clicks an unmined sqaure in row r and column c, the method reveal(r,c) is called. You can find this method at the very end of MineField.java. To complete the second exercise for this lab, you only need to make this method recursive. You do not have to make any changes outside this method.

You will add, maybe, a dozen lines of code. The basic idea is that if the number of mines in neighboring squares is zero, then the method should call itself for each of the eight neighboring positions. However, the method has to be careful not to process a square that has already been revealed, since doing so will lead to an infinite recursion. Note that there is already a method bombCount(r,c) that counts the number of bombs in the neighboring squares around the square at position (r,c).

You can find a complete version of the game, including the recursion, in /classes/s11/cs225/MineSweeperComplete.jar.

If you have previously done a version of MineSweeper that uses recursion, you will want something else to work on. Here are some ideas...

The MineSweeper game creates a random board with a specified number of mines. At least two things can go wrong: First, it is possible that the game is already solved when it is first created. This can only happen after the recursive reveal() method is implemented; once that's done, calling reveal(0,0) to start the game might cause a chain of squares all the way home to be marked. Second, it's possible that there is no solution at all, that is all possible paths from the starting square to the home square are blocked by mines. The first problem is more likely to occur when the number of mines is small, and the second is more likely to occur when the number is large.

When a game is started and the program creates a random board, it calls the method configOK() to check whether the randomly generated board is OK to use for the game. You can find configOK() in the file MineField.java. Currently, this method only checks for the first problem. That is, it checks whether state[ROWS-1][COLS-1] == STATE_REVEALED before the game has even started.

You could make it possible for configOK() to check for the second possible problem as well. That is, you could check whether there is a path of legal moves from the upper left square to the lower right square. This will require a recursive method. It will be similar to the maze-solving algorithm that we will looked at in class. (You will need another boolean array for marking squares.)

(It might be a good idea to add one more test to configOK(): Avoid games that are "almost" already solved to begin with, by making sure that the number of initially visited squares is not too big. Or maybe by making sure that no square that is less than a certain distance from the goal square is initially visited. You might want to add such a test. Note that it would not use recursion.)

Exercise 3: Anagrams

The final exercise is the problem that we have been talking about in class: Given a sequence of letters, find all words that can be made from letters selected from that sequence, in any order.

The program Scramble.java is a starting point for the exercise. The program already reads a list of words from a data file, and it reads in strings of letters from the user. (The data file is a "resource" file, that is, a file that is part of the program but is not a compiled .class file. Resources include things like images, sounds, or data used by the program. In this case, the resource file is assumed to be a file named wordlist.txt in a directory named resources. You can read about resources in Subsection 13.1.3.)

You should write a recursive method to find all the words in a given sequence of letters. As we saw in class, the method can be declared as

         private static void findWords(String input, String stringSoFar, boolean[] used)

and can be called in the main program as

        findWords( text, "", new boolean[text.length()] );

where text is the string of letters that was entered by the user.

You can do the exercise in several parts:

1. Write a findWords method that simply prints out each word as it finds it. You can call the method wordExists(stringSoFar) to check whether a given string is in the list of words. The program at this point should work for a short string, say up to 6 or 7 letters.
2. The wordExists method is horribly inefficient! It uses linear search to search for a word in the word list. However, the word list is in alphabetical order, so binary search would be much more efficient. You should re-write wordExists() to use binary search. (It doesn't have to be recursive!) The program at this point should work for slightly longer strings, say 8 or 10 characters. However, the real inefficiency is in the findWords method, which has run time Θ(n!), where n is the length of the input string.
3. Finally, you should improve findWords as we discussed in class, by testing whether there is any word in wordList that starts with stringSoFar. (If not, there is no use trying to add additional letters onto the string!) You can write another method to make this check. It will almost identical to wordExists, except that instead of looking for an exact match for a given string, it should look for a word that starts with the given string. (The Java String class has a convenient method named startsWith that you can use here.)
4. As an optional extension, you can stop your program from printing out duplicate words. To do that, you will need to store the words in an ArrayList as you find them. If you find a word that is already in the list, don't print it. (Alterntatively, you could save the words without printing anyting as you go along. At the end, you can sort the list of words that you found, before printing its contents, so that the output will be in alphabetical order. If you want to read ahead in the book, you could use a TreeSet instead of an ArrayList.)