The Turing Machine Program

The web appcan be found here:  https://math.hws.edu/eck/js/turing-machine/TM.html.

There is a link on the top of that page to brief Info and Instructions about the program. Mostly, it's reasonably intuitive. Hopefully, you learned enough from the demo on Wednesday to use the program.

It would be a good idea for you to spend some time familiarizing yourself with the program. Try some of the sample machines, and try giving them different inputs to run on. Use the step button to do a computation one step at a time. Click the "New Turing Machine" button, and try to add some rules. Note that if a TM gets into a situation for which it doesn't have a rule, it will stop. At that point, you can define the needed rule, and resume the execution. There is also a "Step Back" button that moves backward through the computation. This can be very useful when you are trying to debug a problem.

Some other remarks: As long as the machine is not running, you can drag the machine on its tape. You can also drag the tape back and forth, taking the machine with it. You can click on the machine and type in a new state number. You can click one of the cells of the tape and type legal symbols onto the tape. If you click inside the rule table, on the value of a "New Symbol", "New State", or "Move", you can type in a new value. But to make a new rule, with a new "Old State" and "Old Symbol", you have to use the Rule Editor. Just select the desired properties for the rule from the popup menus. Finally, note that there is an Undo button and a Redo button to the left of the rules table.

Saving and Turning in your Work

I would like to be able to run any machines that you do for the homework. (Except for very trivial machines, it's difficult to tell what the machine will do by looking at the rule table). You might also want to be able to save partially completed work so that you can return to it later. The Turing Machine program runs in a web browser and therefor it cannot save your work to a file. However, it does have a way of exporting your work.

To save your work, click the button labeled "Show Import/Export," on the bottom left. You will see a popup that can be used to save and reload TM specifications (or even to hand-edit them). One of the buttons in that popup is named "Grab Current Example." Clicking that button will show the definition for the current machine and tape. Here is what it looks like for the "Binary Increment" example machine:

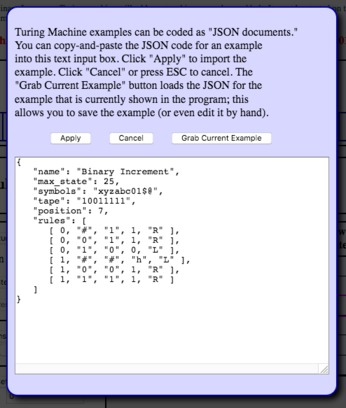
To save your work, use "Show Input/Export" and "Grab Current Example". Select all of the text in the text box, and you paste it into a plain text file, which you can save as usual. It is essential to copy the entire text, including the braces at the beginning and the end. You can turn in the text file containing the definitions of your machines as part of your submission for homework 10. I will copy-and-paste your machines into the program for testing.

If you want to reload your work into the program, go to the program on the web, click "Show Import/Export." Open the text file and select the TM specification. Copy it, and paste it into the text area in the "Show Import/Export" popup. Click "Apply." Your machine will be loaded into the program, just as it was when you saved it.

Preliminary Exercise: Looking for $'s

The rest of this web page has some exercises that you might want to do to get experience working with the program. You do not need to turn in any work that you do for these exercises. The only work that you need to turn in is your solutions for Exercises 5 and 6 in Homework 10.

In class, we looked at a simple example of a Turing machine that moves to the right searching for two $'s in a row. When (and if) it encounters them, it halts, and the machine is left on the second $

Create that Turing machine in the simulator. You can assume that the tape contains only a's, b's, blanks, and $'s.

This can be done using two states (in addition to the halt state), if you use the "stay" option (S) as a direction of motion at the end. Without that option, it requires 3 states to put the machine in the proper position at the end. If you use the "other" and "same" options for "Old Symbol" and "New Symbol" in some of your rules, you can do this with just four or five lines in the rule table.

Preliminary exercise: A Regular Language

Create a Turing machine that checks whether the number of characters in a string of a's and b's is a multiple of 3. The input is a string of a's and b's, with the machine positioned on the left end of the string. The machine can read the string of a's and b's, erasing them as it goes. It can change state to keep track of whether the number of characters that have been encountered is of the form 3n, 3n+1, or 3n+2. When it reaches the end of the string, its current state will tell it whether the number of characters was a multiple of three or not. In the end, the machine should write a 1 on the tape if the number was a multiple of three and should write a 0 on the tape if the number was not a multiple of three. (A 0 or 1 is the required output for a machine that "decides" a language.)

{
   "name": "Decrement",
   "max_state": 25,
   "symbols": "xyzabc01$@",
   "tape": "1011",
   "position": 3,
   "rules": [
      [ 0, "#", "#", 2, "R" ],
      [ 0, "0", "1", 0, "L" ],
      [ 0, "1", "0", 1, "R" ],
      [ 1, "#", "#", "h", "L" ],
      [ 1, "0", "0", 1, "R" ],
      [ 1, "1", "1", 1, "R" ],
      [ 2, "#", "#", "h", "L" ],
      [ 2, "1", "#", 2, "R" ]
   ]
}