A Short Introduction to Metric Spaces:
Section 1: Open and Closed Sets
Our primary example of metric space is $(\R,d),$ where $\R$ is the set of real numbers and $d$ is the usual distance function on $\R,$ $d(a,b) = |a-b|.$ In this metric space, we have the idea of an "open set." A subset of $\R$ is open in $\R$ if it is a union of open intervals. Another way to define an open set is in terms of distance. A set is open in $(\R,d)$ if whenever it contains a number $a,$ it also contains all numbers "sufficiently close" to $a.$ More precisely, a subset $A$ of $\R$ is open in $(\R,d)$ if for every $a\in A,$ there is a number $\varepsilon>0$ such that the open interval $(a-\varepsilon,a+\varepsilon)$ is a subset of $A.$ The open interval $(a-\varepsilon,a+\varepsilon)$ consists of all numbers that are within distance $\varepsilon$ of $a.$ In a general metric space, the analog of the interval $(a-\varepsilon,a+\varepsilon)$ is the "open ball of radius $\varepsilon$ about $a,$" and we can define a set to be open in a metric space if whenever it includes a point $a,$ it also includes an entire open ball of radius $\varepsilon$ about $a.$
Definition 1.1: Let $(M,d)$ be a metric space. For $a\in M$ and $r>0,$ we define the open ball about $a$ of radius $r$ to be the set $B_r(a) = \{x\in M\;|\;d(x,a) < r\}.$
It is possible to have different metrics on the same set. To make it clear what metric is being used, the open ball $B_r(a)$ in a metric space $(M,d)$ can also be written $B_r^d(a)$ when the metric that is being used is not clear from context.
Definition 1.2: Let $(M,d)$ be a metric space, and let $x\in M.$ A subset $A$ of $M$ is said to be a neighborhood of $x$ if there is an $\varepsilon>0$ such that $B_\varepsilon(x)\subseteq A$; that is, if $A$ contains an open ball about $x.$
Definition 1.3: Let $(M,d)$ be a metric space. A subset $X$ of $M$ is said to be open in $(M,d)$ if and only if for every $a\in X,$ there is an $\varepsilon>0$ such that $B_\varepsilon(a)\subseteq X.$ Note that a set is open if and only if it is a neighborhood of each of its points.
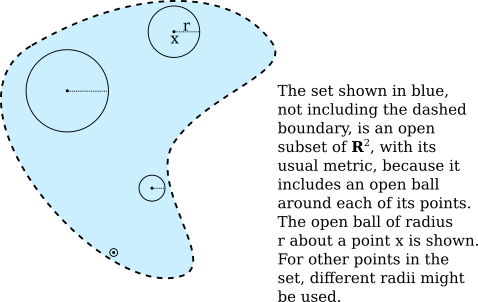
To justify the name "open ball," we should check that an open ball is in fact an open set according to the above definition. This fact can be proved using the triangle inequality:
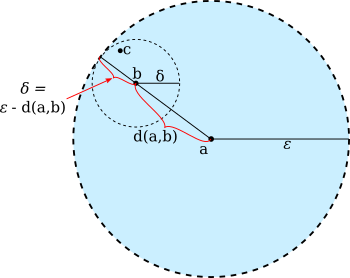
Theorem 1.1: Let $(M,d)$ be a metric space. Let $a\in M$ and $\varepsilon > 0.$ Then the open ball $B_\varepsilon(a)$ is an open set.
Proof: Let $b$ be any point in $B_\varepsilon(a).$ To show $B_\varepsilon(a)$ is open, we must show that there exists $\delta>0$ such that $B_\delta(b)\subseteq B_\varepsilon(a).$ Let $\delta = \frac{1}{2}\big(\varepsilon - d(b,a)\big).$ Since $b\in B_\varepsilon(a),$ we know by definition that $d(b,a) < \varepsilon,$ so that $\delta > 0.$
To show $B_\delta(b)\subseteq B_\varepsilon(a),$ let $c\in B_\delta(b).$ By definition, this means that $d(c,b) < \delta.$ By the triangle inequality, we then have $$\begin{align*} d(c,a) &\le d(c,b) + d(b,a) \\ &< \delta + d(b,a) \\ &= (\varepsilon - d(b,a)) + d(b,a)\\ &= \varepsilon \end{align*}$$ Since $d(c,a)<\varepsilon,$ this shows that $c\in B_\varepsilon(a),$ and since $c$ is any point in $B_\delta(b),$ we have shown that $B_\delta(b)\subseteq B_\varepsilon(a).$ ∎
This picture illustrates the proof:
Theorem 1.2: Let $(M,d)$ be a metric space. Then the open sets in $M$ satisfy the following properties:
- $M$ is open and $\varnothing$ is open;
- the union of any collection (finite or infinite) of open sets is open; and
- the intersection of any finite collection of open sets is open.
Proof: For (1), note that it is vacuously true that the empty set contains an open ball about each of its points, since it contains no points. And the set $M$ contains an open ball about each of its points because every open ball is a subset of $M.$
For (2), suppose that $\{\O_\alpha\,|\,\alpha\in A\}$ is any collection of open sets in $(M,d).$ Let $x\in\bigcup_{\alpha\in A}\O_\alpha.$ We must find an $\varepsilon>0$ such that $B_\varepsilon(x)\subseteq \bigcup_{\alpha\in A}\O_\alpha.$ But since $x$ is in the union of the $\O_\alpha,$ there is some $\beta\in A$ such that $x\in\O_\beta.$ Since $\O_\beta$ is open, there is an $\varepsilon>0$ such that $B_\varepsilon(x)\subseteq\O_\beta.$ Then, since $B_\varepsilon(x)\subseteq\O_\beta$ and $\O_\beta\subseteq\bigcup_{\alpha\in A}\O_\alpha,$ it follows that $B_\varepsilon(x)\subseteq\bigcup_{\alpha\in A}\O_\alpha.$
For (3), suppose that $\{\seq{\O}{n}\}$ is any finite collection of open subsets of $(M,d),$ and let $x\in\bigcap_{i=1}^n\O_i.$ Then $x\in\O_i$ for each $i=1,2,\dots,n.$ So, for each $i,$ there is an $\varepsilon_i>0$ such that $B_{\varepsilon_i}(x)\subseteq \O_i.$ Let $\varepsilon=\min\{\seq{\varepsilon}{n}\}.$ (Note that $\varepsilon>0,$ since it is the minimum of a finite number of positive numbers.) Then $B_\varepsilon(x)\subseteq\O_i$ for all $i,$ which implies that $B_\varepsilon(x)\subseteq\bigcap_{i=1}^n\O_i.$ (This uses the obvious fact that if $r\le s,$ then $B_r(x)\subseteq B_s(x).$) ∎
Since any open interval in $\R$ is an open set in $(\R,d),$ we see that any union of open intervals is open in $(\R,d),$ including infinite unions. It is also true that, conversely, every open set in $(\R,d)$ is a union of open intervals. In fact, it is easy to see that any open set in any metric space is a union of open balls, and an open ball in $(\R,d)$ is an open interval. Note that an infinite intersection of open intervals might or might not be open.
We can also define "closed" sets in a metric space. In $(\R,d),$ we have the idea of a closed interval $[a,b],$ but it is not immediately clear how to define closed sets in general. Note that the complement of the closed interval $[a,b]$ is the open set $(-\infty,a)\cup(b,\infty).$ We use this as a basis for the general definition.
Definition 1.4: Let $(M,d)$ be a metric space. A subset $C$ of a metric space $(M,d)$ is said to be closed in $(M,d)$ if its complement, $M\smallsetminus C,$ is open in $(M,d).$
Note that a set can be both open and closed; for example, the empty set is both open and closed in any metric space. Furthermore, it is possible for a set to be neither open nor closed; for example, in $(\R,d),$ a half-open bounded interval $[a,b)$ is neither open nor closed.
By applying DeMorgan's laws to the previous theorem, we can easily prove the following similar theorem for closed sets:
Theorem 1.3: Let $(M,d)$ be a metric space. Then the closed sets in $M$ satisfy the following properties:
- $M$ is closed and $\varnothing$ is closed;
- the intersection of any collection (finite or infinite) of closed sets is closed; and
- the union of any finite collection of closed sets is closed.
Note carefully that the roles of intersections and unions are reversed for closed sets: An infinite union of open sets is open, but an infinite union of closed sets is not necessarily closed. An infinite intersection of closed sets is closed, but an infinite intersection of open sets is not necessarily open.
We can give an alternative definition of closed set using the idea of "accumulation point" (also known as "cluster point" or "limit point"). An accumulation point of a set is a point that is arbitrarily close to elements of that set.
Definition 1.5: Let $(M,d)$ be a metric space, let $X\subseteq M,$ and let $x\in X.$ Then $x$ is an accumulation point of $X$ if for every $\varepsilon>0,$ $X\cap (B_\varepsilon(x)\smallsetminus \{x\}) \ne \varnothing.$ That is, for any $\varepsilon>0,$ there is at least one element of $X,$ other than $x$ itself, that is within distance $\varepsilon$ of $x.$
Note that an accumulation point of $X$ might or might not be an element of $X.$ For example, consider the metric space $(\R,d),$ where $d$ is the usual metric. The accumulation points of the open interval $X=(0,1)$ are all points in the closed interval $[0,1].$ In this example, every point of $X$ is an accumulation point, and there are two additional accumulation points of $X,$ zero and one, that are not elements of $X.$ The only accumulation point of the set $Y=\{\frac{1}{n}\,|\, n\in {\mathbb N}\}$ is the number zero, so in this case, no accumulation point of $Y$ is an element of $Y.$
For any closed set $X,$ every accumulation point of $X$ is an element of $X.$ In fact, this property characterizes closed sets.
Theorem 1.4: Let $(M,d)$ be a metric space, and let $X\subseteq M.$ $X$ is closed if and only if every accumulation point of $X$ is an element of $X.$
Proof: Suppose first that $X$ is closed. Let $x$ be an accumulation point of $X.$ We need to show that $x\in X.$ Suppose, for that sake of contradiction, that $x\not\in X.$ Then $x$ is in the complement, $M\smallsetminus X.$ Since $X$ is closed, we know by definition of closed that $M\smallsetminus X$ is open. Since $M\smallsetminus X$ is open and $x\in M\smallsetminus X,$ we know by definition of open set that there is an $\varepsilon>0$ such that $B_\varepsilon(x)\subseteq M\smallsetminus X.$ Since $B_\varepsilon(x)$ is entirely contained in the complement of $X,$ the intersection $X\cap B_\varepsilon(x)=\varnothing.$ But this contradicts the fact that $x$ is an accumulation point of $X.$ This contradiction shows that $x\not\in X$ is impossible, and so we must have $x\in X.$
Conversely, suppose that every accumulation point of $X$ is an element of $X.$ We need to show that $X$ is closed. That is, we must show that the complement, $M\smallsetminus X,$ is open. Let $a\in M\smallsetminus X.$ By definition of open, we need to find an $\varepsilon>0$ such that $B_\varepsilon(a)\subseteq M\smallsetminus X.$ Since $a\not\in X$ and every accumulation point of $X$ is in $X,$ it follows that $a$ is not an accumulation point of $X.$ By definition of accumulation point, this means that there is an $\varepsilon>0$ such that $X\cap (B_\varepsilon(a)\smallsetminus \{a\}) = \varnothing.$ Since we also know $a\not\in X,$ we have in fact $X\cap B_\varepsilon(a) = \varnothing,$ which is equivalent to $B_\varepsilon(a) \subseteq M\smallsetminus X. $ ∎
Definition 1.6: Let $(M,d)$ be a metric space, and let $X$ be a subset of $M.$ We define $\overline{X},$ the closure of $X,$ to be the set consisting of all the points of $X$ together with all the accumulation points of $X.$
Theorem 1.5: Let $(M,d)$ be a metric space, and let $X$ be a subset of $M.$ Then $\overline{X}$ is closed.
Proof: By the previous theorem, it suffices to show that $\overline{X}$ contains all of its accumulation points. So, suppose that $x$ is an accumulation point of $\overline{X}.$ We need to show $x\in \overline{X},$ that is, we need to show that either $x\in X$ or or $x$ is an accumulation point of $X.$ In fact, we show that $x$ is an accumulation point of $X.$
Let $\varepsilon>0.$ We need to show that $X\cap (B_\varepsilon(x)\smallsetminus \{x\})\not=\varnothing.$ Since $x$ is an accumulation point of $\overline{X},$ we know that $\overline{X}\cap (B_{\varepsilon/2}\smallsetminus \{x\})\not=\varnothing.$ Let $y\in \overline{X}\cap (B_{\varepsilon/2}\smallsetminus \{x\}).$ Since $y\in \overline{X},$ either $y\in X$ or $y$ is an accumulation point of $X.$ In the case where $y$ is in $X,$ then $y$ is in $X\cap (B_\varepsilon(x)\smallsetminus \{x\})$ and we are done.
Turning to the case where $y$ is an accumulation point of $X.$ Let $\delta = d(x,y).$ Since $y\in B_{\varepsilon/2}(x)$ and $y\ne x,$ $\delta$ is greater than zero and less than $\frac{\varepsilon}{2}.$ Because $y$ is an accumulation point of $X,$ we know that $X\cap (B_\delta(y)\smallsetminus\{y\})\not=\varnothing.$ Let $z \in X\cap (B_\delta(y)\smallsetminus\{y\}).$ Then $$\begin{align*} d(z,x) &\le d(z,y) + d(y,x)\\ &< \delta + d(y,x)\\ &< \frac{\varepsilon}{2}+\frac{\varepsilon}{2}\\ &= \varepsilon. \end{align*}$$ That is, $z\in B_\varepsilon(x).$ Furthermore, $z\not=x$ (since $d(z,y)<\delta<d(x,y)$), and $z\in X.$ That is, $z\in X\cap (B_\varepsilon(x)\smallsetminus\{x\}),$ so that we are done in this case as well. ∎
Note that if $C$ is a closed subset of a metric space, then the fact that $C$ already contains all of its accumulation points means that $\overline{C}=C.$ And if $X$ is any subset of a metric space, the fact that $\overline{X}$ is closed means that $\overline{\overline{X}}=\overline{X}.$
There is another kind of "space" that is even more general than metric space. A topological space is a pair $(X,\cal T)$ where $\cal T$ is a collection of subsets of $X$ satisfying
- $M\in\cal T$ and $\varnothing\in\cal T$;
- the union of any collection of sets in $\cal T$ is again a set in $\cal T$ and
- the intersection of any finite collection of sets in $\cal T$ is again a set in $\cal T.$
The collection $\cal T$ of subsets of $X$ is then said to be a topology for $X,$ Theorem 1.2 shows that the collection of open sets in a metric space $(M,d)$ form a topology for that metric space and make $M$ into a topological space. We will not cover topological spaces here, but I will sometimes note that a property that we are defining for metric spaces is actually a topological property. This means that the property can be defined entirely in terms of open and closed sets, with no mention of any metric. Topological properties of metric spaces can be extended to topological spaces in general. For example, accumulation points can be defined for topological spaces by using an alternative definition that does not mention the metric: A point $x$ is an accumulation point of $X$ if every open set that contains $x$ also contains some point of $X$ other than $x$ itself. This means that the closure of a set is also a topological property, since it is defined in terms of accumulation points.
Exercises
Exercise 1.1: Let $(M,d)$ be a metric space, and let $x\in M.$ Show that the set $\{x\}$ is closed in $(M,d)$ by showing that its complement, $M\smallsetminus\{x\}$ is open. Conclude that any finite subset of a metric space is closed.
Exercise 1.2: Consider the metric space $(\R,d).$ Let $A$ be the interval $[1,2).$ Show that $A$ is not open. (Hint: Consider open balls about 1.) And show that $A$ is not closed by showing that its complement is not open.
Exercise 1.3: Let $(M,d)$ be a metric space. Show that $M$ can be written as a union of open balls.
Exercise 1.4: Consider the metric space $(\R,d).$ For $n=1,2,3,\dots,$ let $\cal O_n$ be the open set $\cal O_n=\big(1,1+\frac{1}{n}\big).$ Show that $\{\cal O_n\,|\,n=1,2,\dots\}$ is an infinite collection of open sets whose intersection is not open. And find an infinite collection of closed subsets of $(\R,d)$ whose union is not closed.
Exercise 1.5: Let $X$ be any set, and define $\delta\colon X\times X\to \R$ by $\delta(a,b) = \begin{cases} 0&\text{if }a=b\\ 1&\text{if }a\not=b\end{cases}.$ Show that $\delta$ is a metric for $X.$ It is called the discrete metric on $X.$ Show that every subset of $X$ is open in the metric space $(X,\delta).$ Hint: What is $B_{1/2}^\delta(x)$? (Note that this implies that every subset of $X$ is also closed in $(X,\delta).$)
Exercise 1.6: Consider the metric space $(\R,d).$ Show that 0 is an accumulation point of the set $X=\{\frac{1}{n}\,|\,n=1,2,3,\dots\}.$ And show that no other point of $\R$ is an accumulation point of $X.$ (Hint: For the second part, consider looking at the cases, $x<0,$ $x>1$ and $\frac{1}{n+1}<x<\frac{1}{n}.$)
Exercise 1.7: What is the closure of the set $X=\{\frac{1}{n}\,|\,n=1,2,3,\dots\}$ in $(\R,d)$? You will need the result of the previous exercise.
Exercise 1.8: Suppose $X$ is a subset of a metric space $(M,d)$ and that $x$ is an accumulation point of $X.$ Let $\varepsilon>0.$ From the definition of accumulation point, we know that $X\cap (B_\varepsilon(x)\smallsetminus \{x\})$ is non-empty. Show that in fact, $X\cap (B_\varepsilon(x)\smallsetminus \{x\})$ is infinite. Hint: Suppose, for the sake of contradiction, that it is finite and show how to find another element of $X\cap (B_\varepsilon(x)\smallsetminus \{x\})$ that is closer to $x$ than any of those finitely many points.
Exercise 1.9: Consider the set $C([a,b]),$ the set of continuous functions on the closed, bounded interval $[a,b].$ Define a metric $\mu$ on this set by $$\mu(f,g) = \int_a^b|f(x)-g(x)|\,dx$$ Show that $\mu$ is in fact a metric. (You will need some facts about integrals and the triangle inequality for the standard metric on $\R$: $|a-c|\le|a-b|+|b-c|$.) For a given $f\in C([a,b])$ and $\varepsilon>0,$ try to describe what it means for a function $g$ to be in $B_\varepsilon^\mu(f).$ (Draw some pictures!)
Exercise 1.10: Suppose that $A$ is a closed, bounded subset of $\R,$ and let $\lambda$ be the least upper bound, $\lambda=lub(A)$. Show that $\lambda\in A.$ Hint: Suppose, for the sake of contradiction, that $\lambda\not\in A,$ and show that in that case, $\lambda$ must be an accumulation point of $A.$ (Similarly, $A$ contains its greatest lower bound.)