Answers for Quiz on Chapter 9
This page contains sample answers to the quiz on Chapter 9 of Introduction to Programming Using Java. Note that generally, there are lots of correct answers to a given question.
Question 1:
Explain what is meant by a recursive subroutine.
Answer:
A recursive subroutine is simply one that calls itself either directly or through a chain of calls involving other subroutines.
Question 2:
Consider the following subroutine:
static void printStuff(int level) {
if (level == 0) {
System.out.print("*");
}
else {
System.out.print("[");
printStuff(level - 1);
System.out.print(",");
printStuff(level - 1);
System.out.print("]");
}
}
Show the output that would be produced by the subroutine calls printStuff(0), printStuff(1), printStuff(2), and printStuff(3).
Answer:
The outputs are:
printStuff(0) outputs: * printStuff(1) outputs: [*,*] printStuff(2) outputs: [[*,*],[*,*]] printStuff(3) outputs: [[[*,*],[*,*]],[[*,*],[*,*]]]
(Explanation: For printStuff(0), the value of the parameter is 0, so the first clause of the if is executed, and the output is just *. For printStuff(1), the else clause is executed. This else clause contains two recursive calls to printStuff(level-1). Since level is 1, level-1 is 0, so each call to printStuff(0) outputs a *. The overall output from printStuff(1) is [*,*]. In a similar way, printStuff(2) includes two recursive calls to printStuff(1). Each call to printStuff(1) outputs [*,*]. And printStuff(2) just takes two copies of this and puts them between [ and ] separated by a comma: [[*,*],[*,*]]. Finally, the output from printStuff(3) outputs two copies of [[*,*],[*,*]] separated by a comma and enclosed between brackets. Once you recognize the pattern, you can do printStuff(N) for any N without trying to follow the execution of the subroutine in detail.)
Question 3:
Suppose that a linked list is formed from objects that belong to the class
class ListNode {
int item; // An item in the list.
ListNode next; // Pointer to next item in the list.
}
Write a subroutine that will count the number of zeros that occur in a given linked list of ints. The subroutine should have a parameter of type ListNode and should return a value of type int.
Answer:
I'll give both a non-recursive solution and a recursive solution. For a linked list, the recursion is not really necessary, but it does nicely reflect the recursive definition of ListNode
static int countZeros( ListNode head ) {
int count; // The number of zeros in the list.
ListNode runner; // For running along the list.
count = 0;
runner = head; // Start at the beginning of the list.
while (runner != null) {
if ( runner.item == 0)
count++; // Count the zero found in the current node.
runner = runner.next; // Advance to the next node.
}
return count;
}
static int countZerosRecursively( ListNode head ) {
if ( head == null) {
// An empty list does not contain any zeros.
return 0;
}
else {
int count = countZerosRecursively( head.next ); // Count zeros in tail.
if ( head.item == 0 )
count++; // Add 1 to account for the zero in the head node.
return count;
}
}
Question 4:
Let ListNode be defined as in the previous problem. Suppose that head is a variable of type ListNode that points to the first node in a linked list. Write a code segment that will add the number 42 in a new node at the end of the list. Assume that the list is not empty. (There is no "tail pointer" for the list.)
Answer:
ListNode tail; // Since no tail pointer is given, we need to make one
tail = head; // We are assuming that this is not null.
while (tail.next != null) {
tail = tail.next;
}
// At this point, tail points to the last node in the list
ListNode node42;
node42 = new ListNode(); // create a new node
node42.item = 42; // the item in the new node is 42
tail.next = node42; // attach the new node to the list
(Explanation: To add a list node at the end of the list, we need a pointer to the last node in the list. Since no such pointer is given, we have to make one. Start with a pointer that is equal to head, and move it down the list until it points to the last node in the list. We know that tail is pointing to the last node in the list if tail.next is null. Use a while loop to move tail down the list until that is true. Then we can make a new node and attach it to the list by setting tail.next to point to it. The value of node42.next is null, and that null marks the new end of the list.)
Question 5:
List nodes can be used to build linked data structures that do not have the form of linked lists. Consider the list node class shown on the left and the code shown on the right:
class ListNode { ListNode one = new ListNode(10);
int item; ListNode two = new ListNode(20);
ListNode next; ListNode three = new ListNode(30);
Listnode(int i) { ListNode four = new ListNode(40);
item = i; one.next = two;
next = null; two.next = three;
} three.next = four;
} four.next = two;
Draw the data structure that is constructed by the code. What happens if you try to print the items in the data structure using the usual code for traversing a linked list:
ListNode runner = one;
while (runner != null) {
System.out.println(runner.item);
runner = runner.next();
}
Answer:
Node one links to node two, node two links to node three, and node three links to node four. If four.next were null, the result would be a normal, four-node linked list. However, node four links back to node two:
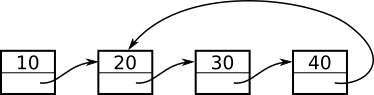
When the while loop is executed, runner will never become null. After the values in the four nodes (10, 20, 30, 40) are printed, the assignment runner = runner.next will set the runner to point to node two again, so the next number printed is 20. The program goes into an infinite loop in which the numbers 20, 30, 40 are printed over and over forever.
Question 6:
What are the three operations on a stack?
Answer:
The three stack operations are push, pop, and isEmpty. The definitions of these operations are: push(item) adds the specified item to the top of the stack; pop() removes the top item of the stack and returns it; and isEmpty() is a boolean-valued function that returns true if there are no items on the stack.
Question 7:
What is the basic difference between a stack and a queue?
Answer:
In a stack, items are added to the stack and removed from the stack on the same end (called the "top" of the stack). In a queue, items are added at one end (the "back") and removed at the other end (the "front"). Because of this difference, a queue is a FIFO structure (items are removed in the same order in which they were added), and a stack is a LIFO structure (the item that is popped from a stack is the one that was added most recently).
Question 8:
What is an activation record? What role does a stack of activation records play in a computer?
Answer:
When a subroutine is called, an activation record is created to hold the information that is needed for the execution of the subroutine, such as the values of the parameters and local variables. This activation record is stored on a stack of activation records. A stack is used since one subroutine can call another, which can then call a third, and so on. Because of this, many activation records can be in use at the same time. The data structure is a stack because an activation record has to continue to exist while all the subroutines that are called by the subroutine are executed. While they are being executed, the stack of activation records can grow and shrink as subroutines are called and return.
Question 9:
Suppose that a binary tree of integers is formed from objects belonging to the class
class TreeNode {
int item; // One item in the tree.
TreeNode left; // Pointer to the left subtree.
TreeNode right; // Pointer to the right subtree.
}
Write a recursive subroutine that will find the sum of all the nodes in the tree. Your subroutine should have a parameter of type TreeNode, and it should return a value of type int.
Answer:
static int treeSum( TreeNode root ) {
// Find the sum of all the nodes in the tree to which root points.
if ( root == null ) {
// The sum of the nodes in an empty tree is zero.
return 0;
}
else {
// Add the item in the root to the sum of the
// items in the left subtree and the sum of the
// items in the right subtree.
int total = root.item;
total += treeSum( root.left );
total += treeSum( root.right );
return total;
}
}
Question 10:
Let TreeNode be the same class as in the previous problem. Write a recursive subroutine that makes a copy of a binary tree. The subroutine has a parameter that points to the root of the tree that is to be copied. The return type is TreeNode, and the return value should be a pointer to the root of the copy. The copy should consist of newly created nodes, and it should have exactly the same structure as the original tree.
Answer:
static TreeNode copyTree( TreeNode root ){
// Make a copy of the tree that root points to.
if (root == null) {
return null; // The copy of an empty tree is an empty tree
}
else {
// The tree is not empty. We need to make a new node
// to be the root of the copy, and then we need to copy
// the left and right subtrees.
TreeNode rootOfCopy = new TreeNode();
rootOfCopy.item = root.item;
rootOfCopy.left = copyTree( root.left );
rootOfCopy.right = copyTree( root.right );
return rootOfCopy;
}
}
(The essential point here is that the subtrees of the original tree can be copied using recursive calls to copyTree(). For example, copyTree(root.left) will make a complete copy of the left subtree of the original tree, and that can become the left subtree of the new root node. This works even if root.left is null.)
Question 11:
What is a postorder traversal of a binary tree?
Answer:
In a traversal of a binary tree, all the nodes are processed in some way. (For example, they might be printed.) In a postorder traversal, the order of processing is defined by the rule: For each node, the nodes in the left subtree of that node are processed first. Then the nodes in the right subtree are processed. Finally, the node itself is processed. This rule is applied at all levels of the tree.
Question 12:
Suppose that a binary sort tree of integers is initially empty and that the following integers are inserted into the tree in the order shown:
5 7 1 3 4 2 6
Draw the binary sort tree that results. Then list the integers in the order that is produced by a post-order traversal of the tree.
Answer:
This picture shows the tree that results after each integer has been inserted, using the treeInsert() method from Subsection 9.4.2:
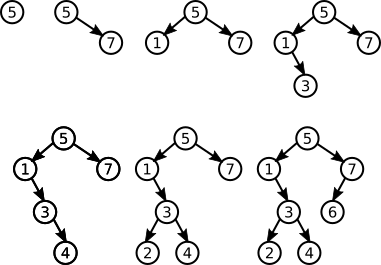
In a post-order traversal, the nodes in the left subtree are processed first, then the nodes in the right subtree, then the root node. For this tree, the nodes are processed in the order:
2 4 3 1 6 7 5
(Of course, an in-order traversal would process the nodes in sorted order: 1, 2, 3, 4, 5, 6, 7.)
Question 13:
Suppose that a <multilist> is defined by the BNF rule
<multilist> ::= <word> | "(" [ <multilist> ]... ")"
where a <word> can be any sequence of letters. Give five different <multilist>'s that can be generated by this rule. (This rule, by the way, is almost the entire syntax of the programming language LISP! LISP is known for its simple syntax and its elegant and powerful semantics.)
Answer:
Here are five possibilities (out of an infinite number of possibilities), with some explanation:
fred — A <multilist> can just be a word, such as "fred".
( ) — The [ ]... around <multilist> means that there can be
any number of nested <multilist>'s, including zero. If
there are zero, then all that's left is the empty
parentheses.
( fred mary chicago )—A <multilist> consisting of three
<multilist>'s—"fred", "mary", and
"chicago"—inside parentheses
( ( able ) ( baker charlie ) )—A <multilist> containing two
<multilist>'s.
( ( a ( b ) ) ( c ( d e ) g ) ) —Even more nesting.
Question 14:
Explain what is meant by parsing a computer program.
Answer:
To parse a computer program means to determine its syntactic structure, that is, to figure out how it can be constructed using the rules of a grammar (such as a BNF grammar).