


| CPSC 120 | Principles of Computer Science | Fall 2025 |
Topics showcase applications of the core concepts, in this case drawing functions and recursion.
Fractals are often used to describe natural things because, like many natural things, fractals have the property of self-similarity — which essentially means that you can zoom in as much as you want and will still see the same basic shape. Realistic modeling of nature is of particular interest in computer graphics.
In this lab, you'll use two different recursive patterns to create fractal models of natural things (tree canopies and mountains).
Successfully completing this topic means that you are able to:
To hand in your sketches:
Make sure that your name and a short description of the sketch are included in a comment at the beginning of each sketch.
Make sure that you've auto-formatted each sketch.
Copy the entire canpoy and mountains (and fractals_ec if you did any extra credit) directories from your sketchbook (~/cs120/sketchbook) to your handin directory (found inside /classes/cs120/handin).
Like labs, topics are individual assignments — what you hand in must be your own work, your own ideas, your own effort. You may get help in office hours and from Teaching Fellows, but you may not work together with a partner or in a group with others to create solutions or write code.
The policies on late work and extensions, academic integrity, and the use of AI for topics are the same as for lab 2. Review the policies there. One extension token is needed for revise-and-resubmit without an initial handin.
Also review assignments and evaluation on the Policies page for how topics factor into the final grade. The short version: topics are optional for a passing grade (C-), but achieving proficiency for at least some topics is required for a higher grade.
Review the slides, examples, and in-class exercises from 11/14 for more about fractals and the additive and substitution patterns.
Visit the Processing API to find out more about specific Processing functions mentioned below, such as dist. You can scroll through the list of all functions on the main API page or use the "filter by keywords..." box to quickly locate a specific function.
Do the exercises in order. Note: following the additive and substitution patterns discussed in class is required for credit — achieving the end result by some other means will not count.
Read through all of each exercise before you start on it. In particular, note that the "to do this" steps are what you should actually do to complete the exercise — don't just read the first sentence of the problem, look at the example, and try to write the sketch from there. Follow the steps!
Put your name and a description of the sketch in comments at the beginning of each sketch. Also don't forget to Auto Format your code before handing it in.
Be sure to save your sketch frequently (ctrl-S). (Every time you run your sketch is good.) The editor does not auto-save!
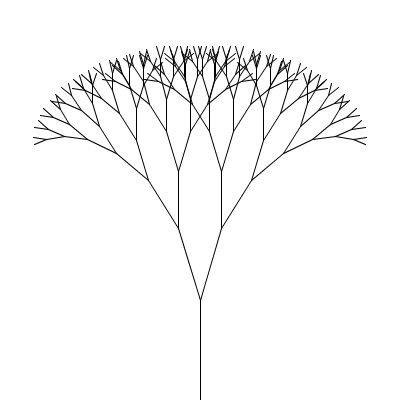
Create a sketch named canopy which draws a fractal canopy as described below. When calling drawCanopy from draw(), use 2*PI/11 for b and 0.75 for s. Size and position the canopy so it fits nicely into your drawing window. (Use -PI/2 as the initial value for a to get the tree standing upright.)
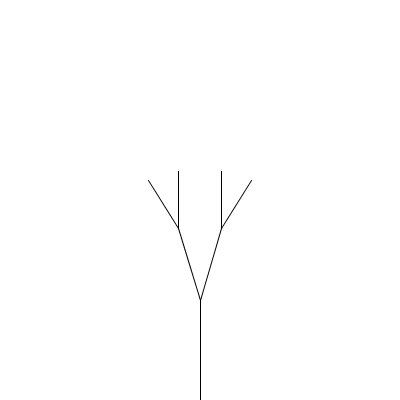
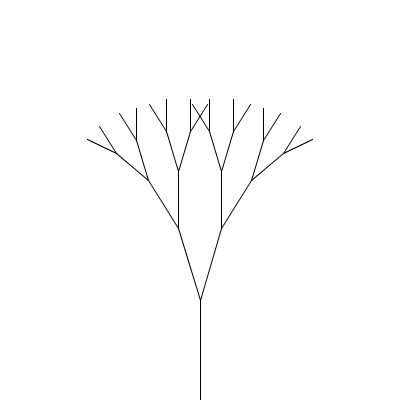
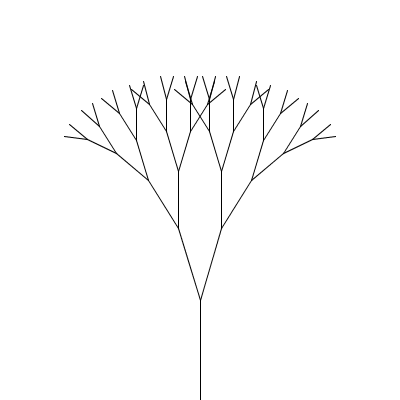
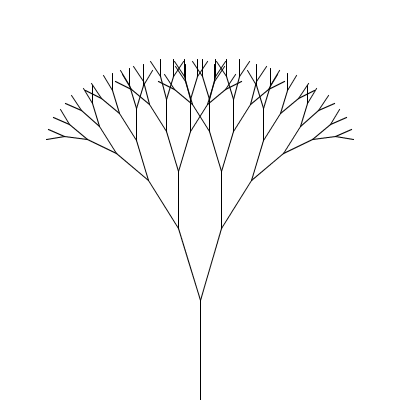
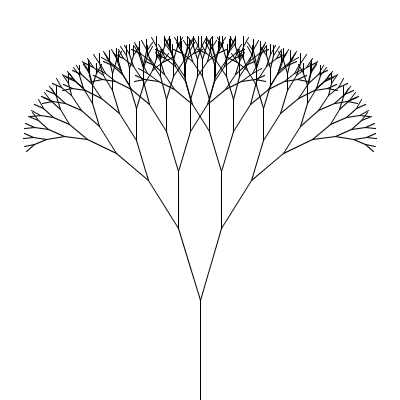
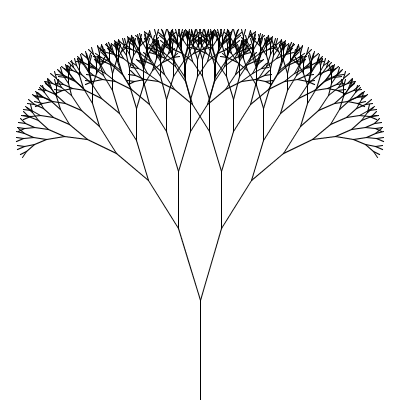
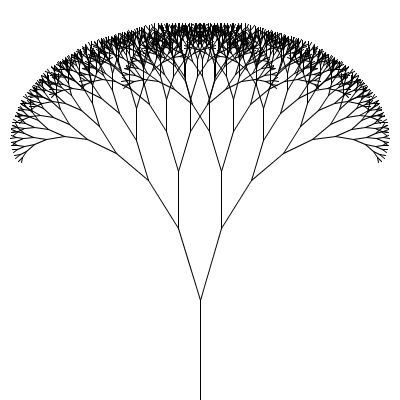
A fractal canopy can be produced by repeatedly adding two shorter line segments at the end of each previous line segment: (click any picture for a larger version)
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
This process follows the additive pattern — each level adds to what was drawn in the previous level. The elements of the pattern:
The whole design is a canopy.
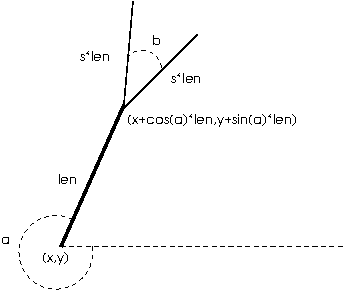
What changes from one level to the next is the position (x,y), length len, and orientation (angle a) of the line segment; the angle b between the two segments in the next level and the scale factor s, which specifies how much the segment lengths shrink from one level to the next, are constant for all levels of a particular canopy but different values can be chosen for different canopies to produce different shapes. All of these things (x, y, len, a, b, and s) should be parameters to the drawCanopy function.
"Small enough" is based on len, the length of the line.
The base shape is a line with endpoints (x,y) and (x+cos(a)*len,y+sin(a)*len).
There are two smaller copies, each with position (x+cos(a)*len,y+sin(a)*len) and length s*len. For the orientation, one copy has angle a-b/2 and the other has angle a+b/2. The angle between segments (b) and the scale factor s stay the same.
Implementation notes:
Use the Processing functions cos and sin to compute cos(a) and sin(a) to find the line endpoints. That means you can write the expressions x+cos(a)*len and y+sin(a)*len exactly as given.
Create a sketch named mountains which draws a fractal mountain range as described below. The mountain range should span the full width of the window. Experiment with the initial value for maxd so that the mountains are suitably rugged (but not too jagged).
Realistic terrain can be generated using a technique known as the midpoint displacement algorithm:

| Start with a line segment connecting two points. (The y coordinates of the points can be equal, as shown in the example, or not.) |
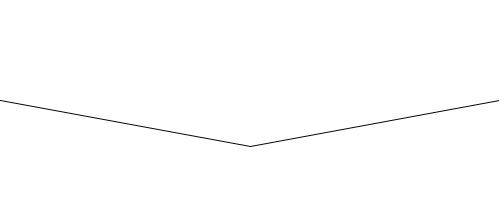
| Replace each line segment with two new line segments which connect the original segment's endpoints with the "displaced midpoint". The displaced midpoint is the midpoint of the original segment moved up or down by a small random amount. |

| Repeat: replace each line segment with two line segments connecting each segment's original endpoints with a displaced midpoint. |

| Repeat: replace each line segment with two line segments connecting each segment's original endpoints with a displaced midpoint. |

| Keep going, until the line segments are sufficiently short. At that point, draw the line segment. |

|
To create solid terrain, replace the final "draw a line segment" step (when the line segments are sufficiently short) with "draw a quad whose top corners are the line segment's endpoints and whose bottom corners are at the bottom edge of the window". The picture below shows an exaggerated view to illustrate this — the red area is the quad associated with the third line segment. 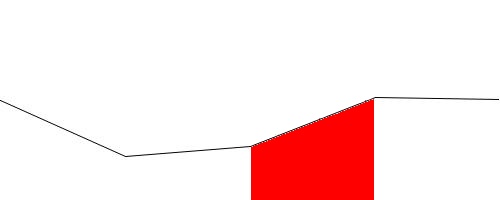
|
The process follows the replacement pattern — the line segment in each level is replaced by the two shorter segments, and only the final line (or quad) is actually drawn. The elements of the pattern:
The whole design is terrain.
What changes from one level to the next are the endpoints (x1,y1) and (x2,y2) of the current segment and the maximum amount the midpoint could be displaced (maxd, for "maximum displacement") — this should decrease with each level to keep the mountains from becoming too jaggedy. (As the line segments get shorter, the displacement needs to get smaller so the lines don't become too steep.) All of these things (x1, y1, x2, y2, and maxd) should be parameters to the drawTerrain function.
"Small enough" is based on the length of the line between (x1,y1) and (x2,y2).
The base shape is a quad whose top corners are (x1,y1) and (x2,y2) and whose bottom corners are at the bottom edge of the window.
There are two smaller copies, one with endpoints (x1,y1) and ((x1+x2)/2,(y1+y2)/2+d) and the other with endpoints ((x1+x2)/2,(y1+y2)/2+d) and (x2,y2) where d is a random value between -maxd and maxd. Both have maximum displacement maxd/2.
Math notes:
Use the Processing function dist to find the distance between two points i.e. the length of the line segment between those points.
Implementation notes:
Use the Processing function random to generate a random value between -maxd and maxd for d.
You will need to create a local variable to store the value for d so that you can use the same value for the two segments. Use the same pattern as with parametric equations — declare, initialize, and use the variable (there is no update) within a new block.
{
float d = ...;
// draw the two smaller copies using d
}
Since each frame involves generating the terrain from scratch, the random number sequence used for the displacements needs to be reproducible. Use the Processing function randomSeed at the beginning of draw() so you don't get jumpy mountains. (It doesn't matter what value you use for the seed, but it needs to be a constant value so it is the same each time draw() is called.)
You can earn extra credit by going substantially beyond the required elements. If you do extra credit, save a copy of your canopy or mountains sketch with the name fractals_ec as a starting point, then modify the copy — don't change your original sketches.
Some possibilities:
Have clicking the mouse decrease the notion of "small enough". (This has the effect of increasing the maximum depth — the pattern will repeat at more levels.) Since "small enough" will now be something that changes over time, you'll need an animation variable for it.
Animate a fractal — for example, you might have a canopy moving around or, more interestingly, try animating it so that it grows more complex over time (deeper levels, not just the whole thing becoming bigger).
Experiment with coloring and/or line thickness (strokeWeight) to make the canopy look more realistic. For example, make the trunk/stem of the canopy brown and only the line segments at the tips green (for leaves).
Add randomness to make the canopy look more realistic: experiment with varying the angle and/or line length by adding a small random amount to the base values. (Choosing a random number in the range -something to something lets the value vary in both directions without having to choose between adding or subtracting.)

Create more of a scene, such as overlapping rows of mountains similar to the picture shown or a combination of mountains and canopy trees. Include multiple instances of mountains and/or canopies.