



F → FF
F → FF
F → FF
| CPSC 120 | Principles of Computer Science | Fall 2025 |
Topics showcase applications of the core concepts, in this case drawing functions and recursion.
Fractals are often used to describe natural things because, like many natural things, fractals have the property of self-similarity — which essentially means that you can zoom in as much as you want and will still see the same basic shape. Realistic modeling of nature is of particular interest in computer graphics.
In this lab, you'll create fractal plants using L-systems.
Successfully completing this topic means that you are able to:
To hand in your sketches:
Make sure that your name and a short description of the sketch are included in a comment at the beginning of each sketch.
Make sure that you've auto-formatted each sketch.
Copy the entire plant1 and plant2 directories from your sketchbook (~/cs120/sketchbook) to your handin directory (found inside /classes/cs120/handin).
Like labs, topics are individual assignments — what you hand in must be your own work, your own ideas, your own effort. You may get help in office hours and from Teaching Fellows, but you may not work together with a partner or in a group with others to create solutions or write code.
The policies on late work and extensions, academic integrity, and the use of AI for topics are the same as for lab 2. Review the policies there. One extension token is needed for revise-and-resubmit without an initial handin.
Also review assignments and evaluation on the Policies page for how topics factor into the final grade. The short version: topics are optional for a passing grade (C-), but achieving proficiency for at least some topics is required for a higher grade.
Review the slides, examples, and in-class exercises from 11/21 for more about L-systems and implementing L-systems in Processing.
Do the exercises in order. Note: following the L-systems pattern discussed in class is required for credit — achieving the end result by some other means will not count.
Read through all of each exercise before you start on it. In particular, note that the "to do this" steps are what you should actually do to complete the exercise — don't just read the first sentence of the problem, look at the example, and try to write the sketch from there. Follow the steps!
Put your name and a description of the sketch in comments at the beginning of each sketch. Also don't forget to Auto Format your code before handing it in.
Be sure to save your sketch frequently (ctrl-S). (Every time you run your sketch is good.) The editor does not auto-save!
Create two sketches plant1 and plant2 to draw two of the L-system plants described below. (One plant per sketch.) At least one of the plants should have two production rules. Choose a reasonable maximum depth. (Start with a small value and increase it incrementally until you find something you like — it doesn't take a very big depth to produce something complex enough to overwhelm the system!) The plant should also be positioned nicely in the sketch window and the length of the line drawn should be such that the plant fits within the window.
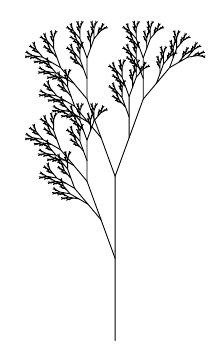
L-systems were introduced in class as a way of describing certain kinds of fractal shapes, such as plants. Several examples of plant L-systems are given below.
 |
 |
 |
 |
 |
|
| angle | 25.7 degrees | 20 degrees | 20 degrees | 25.7 degrees | 22.5 degrees |
| generator | F | F | X | X | X |
| production rule(s) | F → F[+F]F[-F]F | F → F[+F]F[-F][F] | X → F[+X]F[-X]+X F → FF |
X → F[+X][-X]FX F → FF |
X → F-[[X]+X]+F[+FX]-X F → FF |
You may get a mirror image of the picture shown — that's OK. (It's a result of different interpretations of whether a positive angle corresponds to a right or left turn.)
Additional specifications:
For all of these, the scale factor for the length is 1 — the length passed to the drawPlant function will be the length of the line segments making up the plant rather than the size of the plant as such.
The starting point for all of the plants is at the base of the stem with the turtle facing up.
Implementation notes:
For the two-rule plants, recall that our translation of an L-system description into a Processing sketch means a drawing function for each symbol for which there is a production rule — so you'll need two drawing functions. Also recall that only F symbols result in a line being drawn, so functions for other production rules (such as X) will have an empty body for the if ( depth == 0 ) case.
You can earn extra credit by going substantially beyond the required elements. If you do extra credit, save a copy of one of your plant sketches with the name lsys_ec as a starting point, then modify the copy — don't change your original sketches.
Some possibilities:
Add interaction: clicking the mouse should increase the maximum depth. Since the maximum depth will be something that changes over time, you'll need an animation variable for it.
Animate a fractal — for example, you might have a plant moving around or, more interestingly, try animating it so that it grows more complex over time (deeper levels, not just the whole thing becoming bigger).
Include other kinds of fractals generated by L-systems in your scene. Try some of the ones on this page or the ones on pages 9-12 and 17 in The Algorithmic Beauty of Plants (which you can find in the Files section on Canvas). (But not the ones posted as examples from class!) You can also try googling for "L systems" and see what you can turn up. Include a comment identifying the source for your fractal(s).
Experiment with coloring and/or line thickness (strokeWeight) to make the plants look more realistic. For example, make the trunk/stem of the plant brown and only the line segments at the tips green (for leaves).
Add randomness to make the plants look more realistic: experiment with varying the angle and/or line length by adding a small random amount to the base values. (Choosing a random number in the range -something to something lets the value vary in both directions without having to choose between adding or subtracting.)
Read about stochastic L-systems on pages 28-29 in The Algorithmic Beauty of Plants (which you can find in the Files section on Canvas) and implement the one described on page 28 (or another one that you make up or find elsewhere). You can make a choice with a certain probability p by using random to generate a random number between 0 and 1, and then checking whether the number generated is less than p.
Create more of a scene which incorporates multiple instances of fractal plants.