Math 110-02, Fall 2008
Assignment 8: Symmetry Groups

This assignment is based on Sections 5.2 though 5.4 of Symmetry, Shape, and Space, which cover planar symmetry groups: the Rosette Groups (Cyclic C_n and Dihedral D_n); the Frieze groups; and the Wallpaper groups. The assignment also includes a first look at final projects. The assignment is due in class on Monday, October 27 (but this might be postponed until the following Wednesday). You will spend some class time between now and then working on the assignment, but you should also spend some time outside of class. You should also read the book and do the exercises -- even those that are not part of the assignment.

From Section 5.2

Homework exercise 1. What is the symmetry group of a snowflake? Why? (Of course, since a real snowflake has some imperfections, it's not an exact symmetry, but you should think about the symmetry group of a perfect, ideal snowflake.) In addition to answering this question, you should make a paper cutout of a snow crystal shape by folding and cutting a piece of paper, in a similar way to what was done in Exercises 21 and 22 of Section 5.2. (You can do those exercises for practice, but not to turn in.) Tape your snowflake cutout securely to your homework. See more snow crystal photographs at snowcrystals.com.

Homework Exercise 2. Exercises 23 and 24 in Section 5.2 are about cutting a paper disk to create a C_n symmetry. Cut a paper disk that has symmetry group C₄, and tape it securely to your homework. Also, state the general method for cutting a paper disk to create a C_n symmetry (for n greater than or equal to 2).

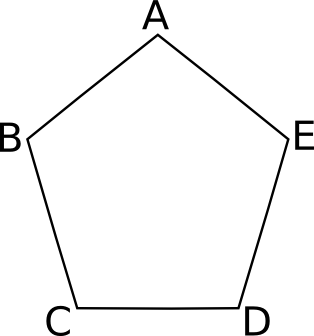Homework Exercise 3. Shown at the right is a regular pentagon, with the vertices labeled with the letters A through E. Let R represent the operation of rotating the pentagon about its center through an angle of 72 degrees. Let F represent the operation of flipping or reflecting the pentagon through the vertical line through its center point.

(a) Draw the pentagon after the operation R has been applied, labeling the vertices with letters to show the new position of each vertex. Also do the same for F.

(b) Draw the pentagon, with labeled vertices, after each of the operations RF and FR.

(c) FR is the same of one of the following: R²F, R³F, or R⁴F. Which one? Why?

(d) Since the symmetry group of the pentagon includes the operation R, it also includes R², R³, R⁴, R⁵, and so on.  What are the angles of rotation for R², R³, R⁴ and R⁵?  What symmetry operation is R⁵ the same as? What about R⁶ and R⁷?  (That is, which of the basic rotations R, R², R³, R⁴, R⁵ are R⁶ and R⁷ the same as?)  R¹³ and R¹⁴?  R¹³⁶ and R¹³⁸?  Devise a general method for dealing with Rⁿ for any positive integer n.

From Section 5.3

Homework Exercise 4. Do Exercise 9 in Section 5.3. That is, determine the symmetry group of each of the frieze patterns in parts (a) through (h) of that exercise. In each case, explain your answer.

Homework Exercise 5. Draw a basic, asymmetrical "motif." Then use your motif in drawings of seven frieze patterns, where each pattern has a different Frieze Group as its symmetry group. You do not have to justify your answers.

Homework Exercise 6. A pattern that consists of an infinite line of upper case A's (...AAAAAAAAAAAA...) has frieze symmetry group pm11 since it has a vertical mirror line, no horizontal mirror line or glide reflection line, and no 180 degree rotation symmetry. What about the other 25 upper case letters? What happens when you consider an infinite line of B's, C's, D's, and so on? For each Frieze Group, list each upper case letter such that an infinite line of that letter has that group as symmetry group.

Homework Exercise 7. Exercises 13 through 17 in Section 5.3 are about cutting strips of paper to exhibit Frieze Group symmetries. You should do these exercises, but do not turn in the resulting paper strips. Just state which of the frieze groups you found in Exercises 13 through 16. Then, for each of the remaining 3 Frieze Groups, give careful and complete instructions on how to fold/roll/cut a long strip of paper to get a pattern that exhibits that symmetry group.

From Section 5.4

Homework Exercise 8. As far as I am concerned, the main point of Section 5.4 is to learn how to determine which wallpaper symmetry group applies to a given pattern. The flow chart at the bottom of page 163 is an algorithm for doing this. You should learn how to use this chart. For practice, you can do the exercises from Section 5.4, especially Exercise 26, but do not turn in your answers to these exercises. Instead, work on the following patterns:

(a)		(b)		(c)
(d)		(e)		(f)
(g)		(h)		(i)
(j)		(k)		(l)

For each of the patterns (a) through (l) shown here, determine the wallpaper symmetry group exhibited by the pattern. For each pattern state the group that applies. Then, choose one pattern from each row -- four patterns in all -- and show in detail how you determined the group. You do not have to justify your answers for the other 8 patterns.

Note that you should ignore imperfections in the patterns -- these are mostly pictures of real objects. You should assume that the pattern is extended to infinity in all directions. Also, it might help to look at the original images on the web, which are in color.

About the Final Project

Homework Exercise 9. Now that we are halfway through the course, it's time to start thinking about your final project. As a first step, you should select two possible topics, and do a little bit of research for each topic. You can choose topics from the list, or you can come up with topics on your own. For each of the two topics, list at least two references for that topic (web addresses acceptable), and write a paragraph about the topic to show that you have done some research on it. (Note that you will not be required to select the actual topic for your project from the two that you research for this homework. At this point, you are just looking into some possibilities.)