A Short Introduction to Metric Spaces
Section 4: Compactness
In the final three sections of this introduction to metric spaces, we will look at three important properties that metric spaces and their subsets can have: compactness, completeness, and connectedness. All of these are generalizations of familiar properties of sets in $(\R,d).$ Any closed, bounded subset of $\R$ is compact. $\R$ itself is the principal example of a complete metric space. And any interval in $\R$ is connected. This section introduces compactness. But before we can even define compactness, we need the concept of an open cover.
Definition 4.1: Let $(M,d)$ be a metric space, and let $X$ be a subset of $M.$ An open cover of $X$ (in $M$) is a collection of open subsets of $M$ such that every point of $X$ is contained in at least one of the open sets in the collection. In other words, an open cover is a set $\{\O_\alpha\,|\,\alpha\in A\}$ of open subsets of $M$ such that $X\subseteq\bigcup_{\alpha\in A}\O_\alpha$ (where $A$ is some index set).
Definition 4.2: Let $X$ be a subset of a metric space $(M,d),$ and suppose that $\mathscr C = \{\O_\alpha\,|\,\alpha\in A\}$ is an open cover of $M.$ A subcover of $X$ from $\mathscr C$ is a subset of $\mathscr C$ that is still an open cover of $X.$ A subcover that is finite is said to be a finite subcover.
Definition 4.3: Let $(M,d)$ be a metric space, and let $K$ be a subset of $M.$ $K$ is said to be a compact subset of $M$ if every open cover of $K$ in $M$ has a finite subcover. If every open cover of $M$ itself has a finite subcover, then $M$ is said to be a compact metric space.
If $K$ is a subset of a metric space $(M,d),$ we seem to have two different meanings for compactness of $K,$ because $K$ can be considered to be a subspace of $(M,d).$ That is, we can consider the metric space $(K,d'),$ where $d'$ is the subspace metric on $K,$ and ask whether $(K,d')$ is a compact metric space. So if I simply say "$K$ is compact," do I mean that $K$ is a compact subset in $(M,d)$ or do I mean that $(K,d')$ is a compact metric space? Fortunately, there is no ambiguity in saying simply that $K$ is compact, because the two conditions are equivalent:
Theorem 4.1: Let $(M,d)$ be a metric space, and let $K$ be a subset of $M.$ Then $K$ is a compact subset of $M$ if and only if the subspace $(K,d')$ is a compact metric space.
Proof: Suppose that $K$ is a compact subset of $M.$ To show that $(K,d')$ is a compact metric space, let $\{U_\alpha\,|\,\alpha\in A\}$ be a collection of open subsets in the metric space $(K,d')$ that covers $K.$ We need to find a finite subcover of $K$ from $\{U_\alpha\,|\,\alpha\in A\}.$ By Theorem 2.1, for each $\alpha,$ there is an open subset $\O_\alpha$ of $M$ such that $U_\alpha = K\cap\O_\alpha.$ The collection $\{\O_\alpha\,|\,\alpha\in A\}$ is then an open cover of $K$ in $M.$ Since $K$ is a compact subset of $M,$ there is finite subcover $\{\O_{\alpha_1},\O_{\alpha_2},\dots,\O_{\alpha_n}\}$ of $K$ from $\{\O_\alpha\,|\,\alpha\in A\}.$ But then $\{U_{\alpha_1},U_{\alpha_2},\dots,U_{\alpha_n}\}$ is a finite subcover of $K$ from $\{U_\alpha\,|\,\alpha\in A\}.$ To see this, let $k\in K.$ Then there is some $i$ such that $k\in\O_{\alpha_i}.$ Since $k\in K$ and $k\in \O_{\alpha_i},$ then $k\in K\cap\O_{\alpha_i}.$ That is, $k\in U_{\alpha_i}.$ So, every element of $k$ is contained in some $U_{\alpha_i}.$
Conversely, suppose that $(K,d')$ is a compact metric space, and let $\{\O_\alpha\,|\,\alpha\in A\}$ be an open cover of $K$ in $M,$ so that each $\O_\alpha$ is an open subset of $M.$ Then, again using Theorem 2.1, $\{K\cap\O_\alpha\,|\alpha\in A\}$ is an open cover of $K$ consisting of open sets in $(K,d').$ This open cover has a finite subcover $\{K\cap\O_{\alpha_i}\,|\,i=1,2,\dots,n\}.$ And it is then clear that $\{\O_{\alpha_i}\,|\,i=1,2,\dots,n\}$ is a finite subcover of $K$ from $\{\O_\alpha\,|\,\alpha\in A\}.$ ∎
As our first example, we show that every bounded, closed interval in $\R$ is compact. This is a special case of the well-known Heine-Borel Theorem, which says that every bounded, closed subset of $\R^n$ is compact. We will not prove the general result here.
Theorem 4.2: Every bounded, closed interval in $\R$ is compact.
Proof: Let $a,b\in\R$ with $a<b,$ and consider the bounded, closed interval $[a,b].$ Suppose that $\mathscr C = \{\O_\alpha\,|\,\alpha\in A\}$ is an open cover of $[a,b]$ in $\R.$ Consider the set $X=\{x\in[a,b]\,|\,$the interval $[a,x]$ has a finite subcover from $\mathscr C\}.$ Now, $a\in\O_\beta$ for some $\beta,$ and therefore $\{\O_\beta\}$ is a finite cover of $[a,a]$ from $\mathscr C.$ So, $a\in X,$ and $X$ is non-empty. Furthermore $X$ is bounded above by $b.$ By the least upper bound axiom, every non-empty subset of $\R$ that is bounded above has a least upper bound. Let $\lambda$ be the least upper bound of $X.$ Note that $a\le \lambda \le b$ because $a\in X$ and $b$ is an upper bound for $X.$ That is, $\lambda\in[a,b].$
We show that $\lambda \in X$ and that $\lambda=b.$ This will finish the proof of the theorem, since by definition of $X,$ it will mean that $[a,b]$ has a finite subcover from $\mathscr C.$
Since $\lambda\in [a,b],$ and $\mathscr C$ is an open cover of $[a,b],$ there is a $\beta\in A$ such that $\lambda\in\O_\beta.$ Since $\O_\beta$ is open, there is an $\varepsilon>0$ such that $(\lambda-\varepsilon,\lambda+\varepsilon)\subseteq\O_\beta.$ Since $\lambda$ is the least upper bound for $X,$ there must be some $x\in X$ such that $x > \lambda-\varepsilon,$ for otherwise, $\lambda-\varepsilon$ would be an upper bound for $X$ that is smaller than $\lambda.$ Since $x\in X,$ there is a finite subcover of $[a,x]$ from $\mathscr C,$ say $\{\O_{\alpha_1},\O_{\alpha_2},\dots,\O_{\alpha_n}\}.$ But then since $[x,\lambda]\subseteq\O_\beta,$ we get a finite subcover of $[a,\lambda]$ by adding $\O_\beta$ to $\{\O_{\alpha_1},\O_{\alpha_2},\dots,\O_{\alpha_n}\}.$ So, by definition of $X,$ $\lambda\in X.$
Finally, we show that $\lambda = b.$ Suppose for the sake of contradiction that $\lambda < b.$ Let $y=\lambda+\frac{1}{2}\min(\varepsilon,b-\lambda).$ Then $y\in\O_\beta$ and therefore $\{\O_\beta,\O_{\alpha_1},\O_{\alpha_2},\dots,\O_{\alpha_n}\}$ is a finite subcover of $[a,y]$ from $\mathscr C.$ And $y\in[a,b],$ because $\lambda<y<b.$ This means $y\in X$ and $\lambda < y.$ But that contradicts the fact that $\lambda$ is an upper bound for $X.$ This contradiction shows that $\lambda=b,$ which finishes the proof. ∎
On the other hand, an open interval in $\R$ is not compact. For example, consider the open interval $(0,1).$ The collection $\{\big(0,1-\frac1n\big)\,|\,n=2,3,4,\dots\}$ is an open cover of $(0,1)$ that has no finite subcover. You are asked to verify this in Exercise 4.1. Similarly, the half-open interval $[0,1)$ is not compact. You might think about what goes wrong if you try to apply the proof of Theorem 4.2 to the set $[0,1).$ In fact, as our next theorem shows, any compact subset of a metric space must be closed. Take careful note of how the finite subcover property is used in the proof; the technique is common in proofs about compactness.
Theorem 4.3: Let $(M,d)$ be a metric space, and supposed that $K$ is a compact subset of $M.$ Then $K$ is a closed subset of $M.$
Proof: We show $K$ is closed by showing that its complement, $M\smallsetminus K,$ is open. Let $z\in M\smallsetminus K.$ We must find an $\varepsilon>0$ such that $B_\varepsilon(z)\subseteq M\smallsetminus K.$ For each $x\in K,$ let $\varepsilon_x=\frac12 d(x,z).$ Since $z\not\in K,$ $\varepsilon_x>0,$ so that $B_{\varepsilon_x}(x)$ is an open set. Note that $x\in B_{\varepsilon_x}(x),$ and $z\not\in B_{\varepsilon_x}(x).$ The collection $\{B_{\varepsilon_x}(x)\,|\, x\in K\}$ is an open cover of $K,$ since any $x\in K$ is covered by the open set $B_{\varepsilon_x}(x).$ Since $K$ is compact, there is a finite subcover $\{B_{\varepsilon_{x_i}}(x_i)\,|\, i = 1,2,\dots,n\}.$ Let $\varepsilon = \min(\varepsilon_{x_1},\varepsilon_{x_2},\dots,\varepsilon_{x_n}\}.$
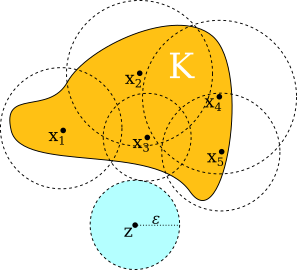
We show that $B_\varepsilon(z)\subseteq M\smallsetminus K,$ which will finish the proof. To show this, let $y\in B_\epsilon(z).$ We want to show $y\in M\smallsetminus K,$ that is, $y\not\in K.$ Consider $x_i,$ where $1\le i\le n.$ By the triangle inequality, $d(x_i,y)+d(y,z)\ge d(x_i,z) = 2\varepsilon_{x_i}.$ So, subtracting $d(y,z)$ from both sides of the inequality, $d(x_i,y)\ge 2\varepsilon_{x_i} - d(y,z) > 2\varepsilon_{x_i} - \varepsilon_{x_i} = \varepsilon_{x_i}.$ (The last inequality follows because $d(y,z)<\varepsilon\le\varepsilon_{x_i}.$) Then, since $d(x_i,y)>\varepsilon_{x_i},$ $y$ is not in the open ball of radius $\varepsilon_{x_i}$ about $x_i.$ Since this is true for every $i$ and the open balls $B_{\varepsilon_{x_i}}(x_i)$ cover $K,$ we have that $y\not\in K.$ ∎
It is also true that every compact set is bounded, but we need a definition of bounded that applies to all metric spaces, not just to $\R.$ "Bounded" should mean that the subset "does not extend to infinity," that is, that it is contained in some open ball around some point. But we will use an equivalent definition, which says that a set is bounded if there is a limit on how far apart two points in the set can be. We can define the "diameter" of such a subset:
Definition 4.4: Let $(M,d)$ be a metric space. A subset $X$ of $M$ is said to be bounded if and only if the set of real numbers $\{d(x,y)\,|\,x,y\in X\}$ is bounded above. For a non-empty bounded set $X,$ we define $diam(X),$ the diameter of $X,$ to be the least upper bound of the set $\{d(x,y)\,|\,x,y\in X\}$ (which exists by the least upper bound property of $\R,$ since the set is bounded above).
Note that by this definition, the empty set is bounded, but we will not attempt to define the diameter of the empty set.
Theorem 4.4: Let $(M,d)$ be a metric space, and supposed that $K$ is a compact subset of $M.$ Then $K$ is bounded.
Proof: If $K$ is empty, then it is bounded. Suppose that $K$ is not empty. Let $x$ be any element of $K,$ and consider the collection of open balls of integral radius, $\{B_i(x)\,|\,i=1,2,\dots\}.$ Since every element of $K$ has some finite distance from $x,$ this collection is an open cover of $K,$ Since $K$ is compact, it has a finite subcover $\{B_{i_1}(x),B_{i_2}(x),\dots,B_{i_n}(x)\},$ where we can assume $i_1<i_2<\cdots<i_n.$ But since $B_{i_1}(x) \subseteq B_{i_2}(x)\subseteq \dots \subseteq B_{i_n}(x),$ this means that $B_{i_n}$ by itself already covers $K.$ Then, for $y,z\in K,$ $y$ and $z$ are in $B_{i_n}(x),$ and $d(y,z)\le d(y,x)+d(x,z) \le i_n + i_n.$ It follows that $2i_n$ is an upper bound for $\{d(y,z)\,|\, y,z\in K\}.$ So, $K$ is bounded. ∎
We have shown that every compact subset of a metric space is closed and bounded. However, the converse does not hold in general. That is, it is not the case that every closed, bounded set is compact. However, that is true for subsets of $\R^n,$ with the usual metric, and this fact gives a complete characterization of compact subsets of $\R^n.$ We will not prove this, but Exercise 4.8 proves it for the case $n=1.$
We turn to another property of compact sets. The Bolzano-Weirstrass Theorem for closed, bounded intervals in $\R$ says that any infinite subset of such an interval has an accumulation point in the interval. A similar result holds for a compact subset of a metric space. The proof is again an application of the finite subcover property.
Theorem 4.5: Let $(M,d)$ be a metric space and let $K$ be a compact subset of $M.$ Then any infinite subset of $K$ has an accumulation point that is an element of $K.$
Proof: We prove the contrapositive. Let $X\subseteq K.$ Assume that $X$ has no accumulation point in $K.$ We must show that $X$ is finite. Let $z\in K.$ Since $z$ is not an accumulation point of $X,$ there is an $\varepsilon_z>0$ such that $X\cap (B_{\varepsilon_z}(z)\smallsetminus\{z\})=\varnothing.$ Thus, $X\cap B_{\varepsilon_z}(z)$ either is empty or is the single point $\{z\}.$ The set of open balls $\{B_{\varepsilon_z}(z)\,|\,z\in K\}$ is an open cover of $K.$ Since $K$ is compact, there is a finite subcover. That is, there are finitely many points $z_1,z_2,\dots,z_n$ such that the corresponding open balls already cover $K.$ But each of the $n$ open balls in that subcover contains at most one point of $X,$ and it follows that $X$ has $n$ or fewer points. So we have proved that $X$ is finite. ∎
Another version of the Bolzano-Weirstrass says that every bounded infinite sequence in $\R$ has a convergent subsequence. We prove an analogous theorem for compact sets.
Theorem 4.6: Let $(M,d)$ be a metric space, and suppose that $K$ is a compact subset of $M.$ Let $\{x_i\}_{i=1}^\infty$ be any sequence of points in $K.$ Then $\{x_i\}_{i=1}^\infty$ has a subsequence that converges to a point in $K.$
Proof: If the terms of the sequence include only finitely many different points of $K,$ then at least one of those points, say $x,$ occurs infinitely often in the sequence. Then $\{x_i\}_{i=1}^\infty$ has a constant subsequence consisting of all the occurrences of $x,$ and that subsequence converges to $x,$ which is in $K$ since every $x_i$ is in $K.$
So, suppose that the terms of the sequence include infinitely many different points in $K.$ Since $K$ is compact, the infinite subset containing all of the terms of the sequence has an accumulation point in $K,$ by the previous theorem. Let $z$ be that accumulation point. We show that $\{x_i\}_{i=1}^\infty$ has a subsequence that converges to $z.$ We use the result from Exercise 1.8, which implies that for any $\epsilon>0,$ the open ball $B_\epsilon(z)$ contains infinitely many of the terms of the sequence. Since $z$ is an accumulation point of the set consisting of all the $x_i,$ there is an index $i_1$ such that $x_{i_1}\in B_1(z).$ Then, since $B_{1/2}(z)$ contains infinitely many terms of the sequence, there is an index $i_2>i_1$ such that $x_{i_2}\in B_{1/2}(z).$ Then, since $B_{1/3}(z)$ contains infinitely many terms of the sequence, there is an index $i_3>i_2$ such that $x_{i_3}\in B_{1/3}(z).$ Proceeding in this way, we obtain indices $i_1 < i_2 < i_3 < \cdots$ such that $x_{i_n}\in B_{1/n}(z)$ for all $n\in\N.$ It follows easily that the subsequence $\{x_{i_n}\}_{n=1}^\infty$ converges to $z.$ ∎
We finish with an important theorem about the relationship between continuity and compactness: The image of a compact set under a continuous function is a compact set.
Theorem 4.7: Let $(A,\rho)$ and $(B,\tau)$ be metric spaces, and let $f\colon A\to B$ be a continuous function. Then for any compact subset $K$ of $A,$ the image $f(K)$ is a compact subset of $B.$
Proof: Let $K$ be a compact subset of $A.$ To show that $f(K)$ is compact, we must show that any open cover of $f(K)$ has a finite subcover. Suppose that $\{\O_\alpha\,|\,\alpha\in I\}$ is an open cover of $f(K)$ in $B.$ By Theorem 3.3, each set $f^{-1}(\O_\alpha)$ is open in $A.$ Furthermore, the collection $\{f^{-1}(\O_\alpha)\,|\,\alpha\in I\}$ covers $K$, since for $k\in K,$ $f(k)\in \O_\beta$ for some $\beta,$ and then $k\in f^{-1}(\O_\beta).$ Since $K$ is compact, it has a finite subcover, $\{f^{-1}(\O_{\alpha_1}),f^{-1}(\O_{\alpha_2}),\dots,f^{-1}(\O_{\alpha_n})\}.$ I claim that $\{\O_{\alpha_1},\O_{\alpha_2},\dots,\O_{\alpha_n}\}$ is a finite subcover of $f(K)$ from $\{\O_\alpha\,|\,\alpha\in I\}.$ In fact, let $b\in f(K).$ That is, $b=f(a)$ for some $a\in K.$ Now, $a\in f^{-1}(\O_{\alpha_i})$ for some $i.$ So, $b=f(a)\in f(f^{-1}(\O_{\alpha_i})) \subseteq \O_{\alpha_i}.$ That is, every element of $f(K)$ is covered by some $\O_{\alpha_i}.$ ∎
Exercises
Exercise 4.1 Show that the open interval $(0,1)$ is not a compact subset of $\R$ by verifying that $\{\big(0,1-\frac1n\big)\,|\,n=2,3,4,\dots\}$ is an open cover of $(0,1)$ that has no finite subcover.
Exercise 4.2 Show that the closed interval $[0,\infty)$ is not a compact subset of $\R$ by finding an open cover of $[0,\infty)$ that has no finite subcover.
Exercise 4.3 Consider a metric space $(X,\delta)$ where $\delta$ is the discrete metric as defined in Exercise 1.5. Let $Y$ be any infinite subset of $X.$ Show that $Y$ is closed and bounded but not compact.
Exercise 4.4 Consider the subspace $\Q$ of $\R.$ That is, consider the metric space $(\Q,d),$ where $d$ is the restriction of the usual metric on $\R$ to $\Q.$ Let $X=\Q\cap[0,1]=\{x\in\Q\,|\,0\le x\le 1\}.$ Show that $X$ is a closed, bounded subset of $(\Q,d)$ that is not compact. Hint: Use Theorem 2.1 for part of the proof.
Exercise 4.5 Let $(M,d)$ be a metric space, and let $X$ be a non-empty subset of $M.$ Show that the following are equivalent:
- $X$ is bounded (in the sense that it has a finite diameter)
- For every $z\in X,$ there is a number $N_z$ such that $X\subseteq B_{N_z}(z).$
- There is a $z\in X$ and a number $N$ such that $X\subseteq B_N(z)$
Hint: The proof of Theorem 4.3 already did part of the work.
Exercise 4.6 A subset $X$ of a metric space is said to be totally bounded if for every $\varepsilon>0,$ $X$ can be covered by a finite collection of open balls of radius $\varepsilon.$ Show that every compact set is totally bounded. Hint: Start with one open ball of radius $\varepsilon$ for every element of $X.$
Exercise 4.7 Let $(M,d)$ be a metric space. Let $K$ be a compact subset of $M,$ and let $C$ be a closed subset of $K.$ Then $C$ is compact. Hint: The set $M\smallsetminus C$ is an open set; try adding this set to an open cover of $C.$
Exercise 4.8 Show that any bounded, closed subset of $\R$ is compact. Hint: Use the previous exercise and Theorem 4.2.
Exercise 4.9 Let $(M,d)$ be a non-empty compact metric space and let $f\colon M\to \R$ be a continuous function (where $\R$ has its usual metric). Show that $f$ achieves a minimum value and a maximum value. That is, there is an $a\in M$ such that for all $x\in M,$ $f(x)\ge f(a),$ and there is a $b\in M$ such that for all $x\in M,$ $f(x)\le f(b).$ This is a generalization of the Extreme Value Theorem. Hint: Use the fact that $f(M)$ is compact, and apply and Exercise 1.10 along with some theorems from this section.
Exercise 4.10 This exercise considers the idea of the distance between sets. Let $(M,d)$ be a metric space, let $X$ and $Y$ be non-empty subsets of $M.$ Define $d(X,Y) = glb\{d(x,y)\,|\,x\in X$ and $y\in Y\}.$ Note that if $X\cap Y \ne \varnothing$ then $d(X,Y)=0.$ Find an example where $X\cap Y = \varnothing$ but $d(X,Y)=0.$ Now suppose that $X$ and $Y$ are non-empty compact subsets of $M.$ Show that $d(X,Y)=0$ if and only if $X\cap Y =\varnothing.$ Hint: Suppose $X\cap Y = \varnothing$ and $y\in Y.$ Then, because $M\smallsetminus X$ is open, there is an $\varepsilon_y>0$ such that $X\cap B_{\varepsilon_y}(y) = \varnothing.$ (Note that the result remains true if we just assume that $X$ is closed and $Y$ is compact.)