A Short Introduction to Metric Spaces
Section 3: Limits and Continuity
The fundamental ideas in calculus include limits and continuity. In this section, we are mainly interested in extending the idea of continuity to functions between arbitrary metric spaces. We will use a definition of continuity that generalizes the definition of continuity for functions from $\R$ to $\R.$ But we will also give two additional properties of functions that are equivalent to continuity, one in terms of infinite sequences and one in terms of open sets. For working with sequences, we will need the idea of "convergence" of an infinite sequence in a metric space to a "limit."
We will use the notation $\seq x$ to denote an infinite sequence. An infinite sequence of points in a set $X$ can be thought of as a function $f\colon\N\to X,$ where $\N$ is the set of natural numbers $\{1,2,3,\dots\}.$ In the notation $\seq x,$ we write $x_n$ instead of $f(n).$
Definition 3.1: Let $(M,d)$ be a metric space. Let $\seq x$ be an infinite sequence of points in $M.$ Let $z\in M.$ We say that the sequence $\seq x$ converges to $z$ if for every $\varepsilon>0,$ there is a natural number $N$ such that $x_n\in B_\varepsilon(z)$ for all $n\ge N.$ In that case we write $\displaystyle \lim_{n\to\infty} x_n = z.$ We say that a sequence in $M$ is convergent if it converges to some point in $M.$
This definition is given in terms of open balls in the metric space. But note that the condition $x_n\in B_\varepsilon(z)$ can be rephrased as $d(x_n,z)<\varepsilon.$ In particular, for the metric space $(\R,d),$ the condition is that $|x_n-z|<\varepsilon,$ so that our definition agrees with the usual definion of convergence of an infinite sequence in $\R.$
In calculus, a function $f\colon\R\to\R$ is said to be continuous at a point $a\in\R$ if for every $\varepsilon>0,$ there is a $\delta>0$ such that for all $x\in\R,$ $|x-a|<\delta$ implies $|f(x)-f(a)|<\varepsilon.$ We could rephrase $|x-a|<\delta$ as $d(x,a)<\delta,$ where $d$ is the usual metric on $\R,$ and $d(x,a)<\delta$ is in turn equivalent to $x\in B_\delta(a).$ This observation lets us extend the idea of continuity to functions between metric spaces.
Definition 3.2: Let $(A,\rho)$ and $(B,\tau)$ be metric spaces, and let $f$ be a function $f\colon A\to B.$ Let $a\in A.$ We say that $f$ is continuous at $a$ if for every $\varepsilon>0,$ there is a $\delta>0$ such that $f(B_\delta^\rho(a))\subseteq B_\varepsilon^\tau(f(a)).$ For a subset $X$ of $A,$ we say that $f$ is continuous on $X$ if $f$ is continuous at $x$ for every $x\in X.$ We say that $f$ is continuous if $f$ is continuous at every point of $A.$
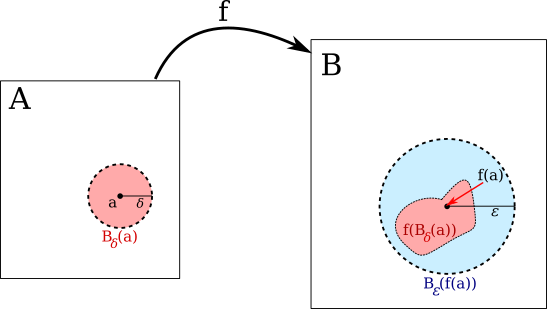
Again, although we have defined continuity using open balls, we can give an equivalent definition in terms of distance: The function $f\colon A\to B$ is continuous at $a\in A$ if for every $\varepsilon>0,$ there is a $\delta>0$ such that for all $x\in A,$ $\rho(x,a)<\delta$ implies $\tau(f(x),f(a))<\varepsilon.$ This definition is closer to the definition of continuity for functions from $\R$ to $\R,$ but the definition that uses open balls is simpler.
Our first alternative characterization of continuity is in terms of convergent sequences: A function is continuous if and only if it preserves convergence of sequences. More formally, we have:
Theorem 3.1: Let $(A,\rho)$ and $(B,\tau)$ be metric spaces, and let $f$ be a function $f\colon A\to B.$ Let $a\in A.$ Then $f$ is continuous at $a$ if and only if for every sequence $\{a_i\}_{i=1}^\infty$ in $A$ that converges to $a,$ the sequence $\{f(a_i)\}_{i=1}^\infty$ in $B$ converges to $f(a).$
Proof: Suppose that $f$ is continuous at $a,$ and let $\{a_i\}_{i=1}^\infty$ be a sequence in $A$ that converges to $a.$ We must show that $\{f(a_i)\}_{i=1}^\infty$ converges to $f(a).$ Let $\varepsilon>0.$ We need to find $N$ such that $f(a_i)\in B_\varepsilon^\tau(f(a))$ for all $i \ge N.$ Since $f$ is continuous at $a,$ there is a $\delta>0$ such that $f(B_\delta^\rho(a))\subseteq B_\varepsilon^\tau(f(a)).$ Since the sequence $\{a_i\}_{i=1}^\infty$ converges to $a$ and $\delta>0,$ there is an $N$ such that $a_i\in B_\delta^\rho(a)$ for all $i\ge N.$ Then, for any $i\ge N,$ the facts that $a_i\in B_\delta^\rho(a)$ and that $f(B_\delta^\rho(a))\subseteq B_\varepsilon^\tau(f(a))$ together show that $f(a_i)\in B_\varepsilon^\tau(f(a)),$ which is what we needed to prove.
For the only-if part, we prove the contrapositive. Suppose that $f$ is not continuous at $a.$ We must show that it is not the case that for every sequence $\{a_i\}_{i=1}^\infty$ in $A$ that converges to $a,$ it follows that $\{f(a_i)\}_{i=1}^\infty$ converges to $f(a).$ We do this by constructing a sequence $\{a_i\}_{i=1}^\infty$ in $A$ that converges to $a,$ but $\{f(a_i)\}_{i=1}^\infty$ does not converge to $f(a).$
Since $f$ is not continuous at $a,$ there is an $\varepsilon>0$ such that for every $\delta>0,$ $f(B_\delta^\rho(a))\not\subseteq B_\varepsilon^\tau(f(a)).$ For each $i\in\N,$ letting $\delta=\frac{1}{i},$ we have that $f(B_{1/i}^\rho(a))\not\subseteq B_\varepsilon^\tau(f(a))$; thus, there must be some $a_i\in B_{1/i}^\rho(a)$ such that $f(a_i)\not\in B_\varepsilon^\tau(f(a)).$ Then the sequence $\{a_i\}_{i=1}^\infty$ converges to $a$ (because given any $\delta>0,$ we can choose an integer $N>\frac{1}{\delta},$ and we then have for $i\ge N$ that $\frac1i\le \frac1N < \delta$ and therefore $a_i\in B_{1/i}^\rho(a)\subseteq B_\delta^\rho(a)$ for all $i>N$). However, the sequence $\{f(a_i)\}_{i=1}^\infty$ does not converge to $f(a)$ (because for every $i\in\N,$ $f(a_i) \not\in B_\varepsilon^\tau(f(a))$). ∎
One nice application of the sequential characterization of continuity is an easy proof that the composition of continuous functions is continuous.
Theorem 3.2: Let $(A,\rho),$ $(B,\tau),$ and $(C,\sigma)$ be metric spaces. Let $f\colon A\to B$ and $g\colon B\to C.$ Let $a\in A.$ If $f$ is continuous at $a$ and $g$ is continuous at $f(a),$ then the composition $g\circ f$ is continuous at $a.$
Proof: Let $\{a_i\}_{i=1}^\infty$ be any sequence in $A$ that converges to $a.$ Since $f$ is continuous at $a,$ the sequence $\{f(a_i)\}_{i=1}^\infty$ converges to $f(a).$ Since $g$ is continuous at $f(a),$ the sequence $\{g(f(a_i))\}_{i=1}^\infty$ converges to $g(f(a)),$ which is $g\circ f(a).$ Since this is true for any sequence in $A$ that converges to $a,$ $g\circ f$ is continuous at $a.$ ∎
Our second characterization of continuity is in terms of open sets. The fact that continuity can be defined without using the metrics shows that it is really a topological rather than a metric property. The theorem can be stated most cleanly in terms of continuity on an entire metric space. In the proof, we use the fact that if $f$ is a function $f\colon A\to B,$ then $f(f^{-1}(Y))\subseteq Y$ for all $Y\subseteq B,$ and $X\subseteq f^{-1}(f(X))$ for all $X\subseteq A.$
Theorem 3.3: Let $(A,\rho)$ and $(B,\tau)$ be metric spaces, and let $f$ be a function $f\colon A\to B.$ Then $f$ is continuous if and only if for every open subset $\O$ of $B,$ the inverse image $f^{-1}(\O)$ is open in $A.$
Proof: Suppose $f$ is continuous, and $\O$ is an open subset of $B.$ We need to show that $f^{-1}(\O)$ is open in $A.$ Let $a\in f^{-1}(\O).$ We need to find an open ball about $a$ that is contained in $f^{-1}(\O).$ By definition of $f^{-1}(\O),$ we have that $f(a)\in \O.$ Since $\O$ is open, there is an $\varepsilon>0$ such that $B_\varepsilon^\tau(f(a))\subseteq \O.$ Since $f$ is continuous at $a,$ there is a $\delta>0$ such that $f(B_\delta^\rho(a))\subseteq B_\varepsilon^\tau(f(a)).$ But then, $B_\delta^\rho(a)\subseteq f^{-1}(f(B_\delta^\rho(a))) \subseteq f^{-1}(B_\varepsilon^\tau(f(a))\subseteq f^{-1}(\O).$ So we have found an open ball about $a$ that is contained in $f^{-1}(\O).$
Conversely, suppose that $f^{-1}(\O)$ is open in $A$ for every open subset $\O$ of $B.$ We must show $f$ is continuous. Let $a\in A.$ To show $f$ is continuous at $a,$ let $\varepsilon>0.$ We must find a $\delta>0$ such that $f(B_\delta^\rho(a))\subseteq B_\varepsilon^\tau(f(a).$ But $B_\varepsilon^\tau(f(a))$ is an open subset of $B,$ and it follows by our assumption that $f^{-1}(B_\varepsilon^\tau(f(a)))$ is open in $A.$ Now, $a\in f^{-1}(B_\varepsilon^\tau(f(a))),$ so there is a $\delta>0$ such that $B_\delta^\rho(a) \subseteq f^{-1}(B_\varepsilon^\tau(f(a))).$ But then $f(B_\delta^\rho(a))\subseteq f(f^{-1}(B_\varepsilon^\tau(f(a)))) \subseteq B_\varepsilon^\tau(f(a)).$ ∎
This characterization of continuity gives another easy proof that the composition of continuous functions is continuous. The proof is left as an exercise.
Exercises
Exercise 3.1: Let $(A,\rho)$ and $(B,\tau)$ be metric spaces, and let $f$ be a function $f\colon A\to B.$ Let $a\in A.$ Verify that the condition that $f(B_\delta^\rho(a))\subseteq B_\varepsilon^\tau(f(a))$ is equivalent to the condition that for all $x\in A,$ $|x-a|<\delta$ implies $|f(x)-f(a)|<\varepsilon.$
Exercise 3.2: For a function $f\colon A\to B,$ verify that $f(f^{-1}(Y))\subseteq Y$ for all $Y\subseteq B,$ and that $X\subseteq f^{-1}(f(X))$ for all $X\subseteq A.$
Exercise 3.3: Let $X$ be any set, and Consider the metric space $(X,\delta)$ where $\delta$ is the discrete metric, $\delta\colon X\times X\to \R$ by $\delta(a,b) = \begin{cases} 0&\text{if }a=b\\ 1&\text{if }a\not=b\end{cases}\;.$ Suppose that $\{x_i\}_{i=1}^\infty$ is a convergent sequence in the metric space $(X,\delta).$ Show that there is a number $N$ such that $x_N=x_{N+1}=x_{N+2}=\cdots$. (We say that the sequence is "eventually constant.")
Exercise 3.4: Let $(X,\delta)$ be the discrete metric space from the previous exercise, and let $(M,d)$ be any metric space. Show that any function $f\colon X\to M$ is continuous. (There are at least three possible proofs: using the definition of continuity, using Theorem 3.1, or using Theorem 3.3.)
Exercise 3.5: Let $\{x_n\}_{n=1}^\infty$ be a convergent sequence in a metric space. Show that its limit is unique. That is, prove the following statement: if $\{x_n\}_{n=1}^\infty$ also converges to $y$ and $\{x_n\}_{n=1}^\infty$ converges to $z,$ then $y=z.$
Exercise 3.6: Define $f\colon \R\to\R$ by $f(x)=\begin{cases}x&\text{ if $x \le 1$}\\x+1&\text{ if $x > 1$}\end{cases}.$ We know from calculus that $f$ is not continuous at 1, so it must fail the continuity tests in Therorems 3.1 and 3.3. Find a sequence $\{x_i\}_{i=1}^\infty$ that converges to 1, but $\{f(x_i)\}_{i=1}^\infty$ does not converge to $f(1).$ And find an open subset $\O$ of $\R$ such that $f^{-1}(\O)$ is not open. ($\R$ here has its usual metric.)
Exercise 3.7: Let $(M,d)$ be a metric space, and let $f\colon M\to \R$ and $g\colon M\to \R$ be two functions from $M$ to $\R$ (where $\R$ has its usual metric). Let $a\in M$. Suppose $f$ and $g$ are continuous at $a$. Show that the function $f+g$ is continuous at $a,$ where $(f+g)(x) = f(x) + g(x)$ for $x\in M.$ Hint: Just imitate the proof for functions from $\R$ to $\R.$
Exercise 3.8: Use Theorem 3.3 to prove that the composition of continuous functions between metric spaces is continuous.
Exercise 3.9: Suppose that $(A,\rho)$ and $(B,\tau)$ are metric spaces and $f\colon A\to B$ is a continuous functions. Define $g\colon A\to f(A)$ by $g(x) = f(x)$ for $x\in A.$ Show that $g$ is a continous function from the metric space $(A,\rho)$ to the subspace $(f(A),\tau')$ of $(B,\tau).$
Exercise 3.10: Let $(M,d)$ be a metric space and let $X\subseteq M$. Show that the closure of $X$ can be characterized as follows: For $z\in M,$ $z \in \overline{X}$ if and only if there is a sequence $\seq x$ of points of $X$ such that $\displaystyle \lim_{n\to\infty}x_n = z.$ Hint: Treat separately the cases where $z\in X$ and where $z$ is an accumulation point of $X.$ (So, if we were to define a limit point of $X$ to be a point $z\in M$ such that $z$ is a limit of some infinite sequence of points of $X,$ then we would have that the closure of a set $A$ consists of all the limit points of $A$. Note, however, that the term "limit point" is more usually used as a synonym for "accumulation point.")